Dynamics on locally homogeneous spaces
Manfred Einsiedler
Abstract.
Let 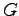 be a closed subgroup of
be a closed subgroup of
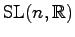 ,
and let
,
and let 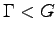 be a discrete subgroup. Then any subgroup
be a discrete subgroup. Then any subgroup 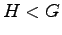 defines a dynamical system on
defines a dynamical system on
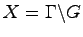 by right
translation. These systems are often considered because of their
intimate connection to problems in number theory. E.g. the dynamics
of
by right
translation. These systems are often considered because of their
intimate connection to problems in number theory. E.g. the dynamics
of
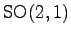 on
on
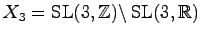 was used by Margulis in his solution to the Oppenheim conjecture.
Marina Ratner later showed many strong structure theorems about
invariant measures, orbit closures, and equidistribution of a general
class of subgroups (thus solving the Raghunathan-Dani conjectures). In
the first part of the course we will discuss these results as well as
their connection to some problems in number theory, and prove some
special cases.
was used by Margulis in his solution to the Oppenheim conjecture.
Marina Ratner later showed many strong structure theorems about
invariant measures, orbit closures, and equidistribution of a general
class of subgroups (thus solving the Raghunathan-Dani conjectures). In
the first part of the course we will discuss these results as well as
their connection to some problems in number theory, and prove some
special cases.
The above result says nothing about the dynamics of the diagonal
subgroup 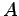 in
in
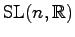 acting on
acting on
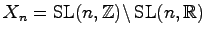 .
Furstenberg, Katok and Spatzier, as well as Margulis conjectured that
some of the above results should also hold for this action. Currently
there is only a partial classification of invariant measures known.
However, this is already enough for several applications to number
theoretic problems. In the second part of the course we will discuss
some of these more recent results.
.
Furstenberg, Katok and Spatzier, as well as Margulis conjectured that
some of the above results should also hold for this action. Currently
there is only a partial classification of invariant measures known.
However, this is already enough for several applications to number
theoretic problems. In the second part of the course we will discuss
some of these more recent results.
Background assumed:
We will assume only minimal knowledge about Lie groups, e.g. Chapter
0 of Knapp's book "Lie groups beyond an introduction" and the basic
theorems from ergodic theory: Poincare recurrence, mean and pointwise
ergodic theorems. Especially for the second part prior knowledge of
entropy would be desirable, but this we will discuss briefly. As a
preparation we recommend Walters "An Introduction to Ergodic Theory",
or whatever chapters of Einsiedler-Ward "Ergodic Theory: with a view
towards Number Theory" are already available (see
http://www.mth.uea.ac.uk/ergodic/).
![]() in
in
![]() acting on
acting on
![]() .
Furstenberg, Katok and Spatzier, as well as Margulis conjectured that
some of the above results should also hold for this action. Currently
there is only a partial classification of invariant measures known.
However, this is already enough for several applications to number
theoretic problems. In the second part of the course we will discuss
some of these more recent results.
.
Furstenberg, Katok and Spatzier, as well as Margulis conjectured that
some of the above results should also hold for this action. Currently
there is only a partial classification of invariant measures known.
However, this is already enough for several applications to number
theoretic problems. In the second part of the course we will discuss
some of these more recent results.