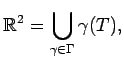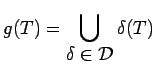Fractal crystallographic tilings
Benoît Loridant
Vienna University of Technology & University Leoben, Austria
A compact set  tiles the plane with respect to a countable group of
isometries
tiles the plane with respect to a countable group of
isometries 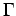 containing the identity map if
containing the identity map if
where the pieces
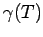 can only intersect at their boundaries. We are interested in sets
can only intersect at their boundaries. We are interested in sets 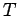 having
also the
property that an expanding affinity
having
also the
property that an expanding affinity 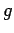 blows up
blows up 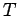 onto a finite
union of some of its isometric copies, i.e.,
for some finite digit set
onto a finite
union of some of its isometric copies, i.e.,
for some finite digit set
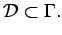 This endows the
tile
This endows the
tile 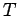 with a
self-similar structure. We wonder when it is homeomorphic to a closed disk.
In fact, the topology of
with a
self-similar structure. We wonder when it is homeomorphic to a closed disk.
In fact, the topology of 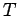 is closely related to the configuration of
the pieces it intersects in the tiling (its neighbors).
The data
is closely related to the configuration of
the pieces it intersects in the tiling (its neighbors).
The data
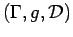 completely
determines the neighbors: they can be computed algorithmically.
Several easily checkable criteria of disk-likeness for
completely
determines the neighbors: they can be computed algorithmically.
Several easily checkable criteria of disk-likeness for
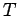 will be given, involving graphs in the general case, or the shape and
number of the neighbors in particular cases.
will be given, involving graphs in the general case, or the shape and
number of the neighbors in particular cases.
Supported by the Austrian Science Foundation (FWF), projects Nr. S9604, S9610,
and S9612.
![]() tiles the plane with respect to a countable group of
isometries
tiles the plane with respect to a countable group of
isometries ![]() containing the identity map if
containing the identity map if