We start with some notation and definitions.
A word is a function ![]() from a finite or infinite block of integers
from a finite or infinite block of integers
![]() to
to ![]() . We call a word
. We call a word ![]() finite when
finite when ![]() is finite and infinite
otherwise.
If
is finite and infinite
otherwise.
If ![]() and
and ![]() we say
we say ![]() has the letter
has the letter ![]() at position
at position ![]() .
If a word
.
If a word ![]() is finite, we denote by
is finite, we denote by ![]() the number of occurrences of the
letter
the number of occurrences of the
letter ![]() in
in ![]() .
.
A word ![]() is called balanced if
is called balanced if
![]() for all subwords
for all subwords
![]() of equal length of
of equal length of ![]() . A finite word
. A finite word ![]() is called strongly
balanced if
is called strongly
balanced if ![]() is balanced. Here
is balanced. Here ![]() is the concatenation of
is the concatenation of ![]() with
with
![]() . An example of a strongly balanced word is
. An example of a strongly balanced word is ![]() . An infinite word is
Sturmian if it is balanced and not ultimately periodic.
. An infinite word is
Sturmian if it is balanced and not ultimately periodic.
A substitution ![]() is an application from
is an application from ![]() to the set of
finite words. It extends to a morphism by concatenation, that is,
to the set of
finite words. It extends to a morphism by concatenation, that is,
![]() . It also extends in a natural way to a map from
infinite words to infinite words.
We call
. It also extends in a natural way to a map from
infinite words to infinite words.
We call
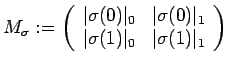 the incidence matrix corresponding to the substitution
the incidence matrix corresponding to the substitution ![]() . A
fixed point of a substitution
. A
fixed point of a substitution ![]() is an infinite word
is an infinite word ![]() with
with
![]() .
.
We call a substitution ![]() Sturmian if
Sturmian if ![]() maps every Sturmian word to a Sturmian word. An example of a Sturmian substitution is
maps every Sturmian word to a Sturmian word. An example of a Sturmian substitution is
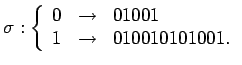
Now we will explain how to form a new word ![]() from a strongly balanced word
from a strongly balanced word
![]() .
If
.
If
![]() is a strongly balanced word with
is a strongly balanced word with
![]() , we define the cutting points corresponding to
, we define the cutting points corresponding to ![]() by
by
![]() .
These cutting points approximate a line piece between the origin and
.
These cutting points approximate a line piece between the origin and ![]() quite well.
We can project the cutting points parallel to this line piece, onto the
quite well.
We can project the cutting points parallel to this line piece, onto the
![]() -axis.
We call
-axis.
We call ![]() the value such that the projection of the
the value such that the projection of the ![]() th cutting point has
the smallest positive
th cutting point has
the smallest positive ![]() -coordinate. Next we replace the projection of each
cutting point
-coordinate. Next we replace the projection of each
cutting point ![]() with 0 or 1, depending on whether
with 0 or 1, depending on whether ![]() is smaller than
is smaller than ![]() or not, and form a word
or not, and form a word ![]() by writing down the zeros and ones in the order
that they appear on the
by writing down the zeros and ones in the order
that they appear on the ![]() -axis, from the top down.
-axis, from the top down.
Our main result is the following.
Let ![]() be a Sturmian substitution that has incidence matrix with
determinant 1 and a fixpoint starting with 0. Let
be a Sturmian substitution that has incidence matrix with
determinant 1 and a fixpoint starting with 0. Let
![]() , and
, and ![]() the word constructed from
the word constructed from ![]() in the way described above. Then there exists a
Sturmian substitution
in the way described above. Then there exists a
Sturmian substitution ![]() such that
such that
![]() for every
for every ![]() .
.