The sum of digits of primes in $ \mathbb{Z}[{\mathrm i}]$

Thomas Stoll

Institut für Diskrete Mathematik und Geometrie, Technische Universität Wien, Austria

Coauthor(s): Michael Drmota, Joël Rivat

Let $ q=-a\pm {\mathrm i}$ (choose a sign) with $ a\in\mathbb{Z}^+$. It is well-known that every $ z\in\mathbb{Z}[{\mathrm i}]$ has a unique finite representation

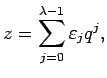
$\displaystyle z=\sum_{j=0}^{\lambda-1} \varepsilon_j q^j,$

where $ \varepsilon_j\in\{0,1,\ldots,a^2\}$ are the digits in the digital expansion of $ z$ and $ \varepsilon_{\lambda-1}\neq 0$. Denote by $ s_q(z)=\sum_{j=0}^{\lambda-1}\varepsilon_j$ the sum-of-digits function in $ \mathbb{Z}[{\mathrm i}]$.



The aim of the present talk is to study the distribution of $ s_q(p)$ in arithmetic progressions, where $ p$ runs through the Gaussian primes. Also, the question is posed whether the sequence $ (\alpha s_q(p))$ is uniformly distributed mod $ 1$, where $ \alpha\in\mathbb{R}$ with $ (a^2+2a+2)\alpha\not\in\mathbb{Z}$. By Weyl's criterion, this means that we are interested in a non-trivial upper bound for the exponential sum

$\displaystyle \sum_{\substack{\vert z\vert^2<N z\in\mathbb{Z}[{\mathrm i}]}} \Lambda_{{\mathrm i}}(z) \mathrm{e}(\alpha s_q(z)),$

where $ \Lambda_i(z)$ denotes the complex Von Mangoldt function. The investigation is inspired by recent results of Mauduit and Rivat for the real sum-of-digits function [MR05].



The approach is as follows: We start with a Vaughan-type inequality and use van der Corput's inequality to split the multiplicative structure of the original exponential sum in order to get a difference process. Next we introduce a truncated version of $ s_q(z)$, whose periodicity properties are well studied with the help of the addition automaton [GKP98]. This in turn allows to use classical Fourier analysis arguments in the upcoming estimates for both the type I- and type II- sums in Vaughan's inequality. We will discuss the state of the art of this investigation and outline possible extensions.

Supported by the Austrian Science Foundation (FWF), project S9604, ``Analytic and Probabilistic Methods in Combinatorics''



[GKP98] P. J. Grabner, P. Kirschenhofer and H. Prodinger, The sum-of-digits function for complex bases, J. London Math. Soc. (2) 57 (1998), no. 1, 20-40.

[MR06] C. Mauduit and J. Rivat, Sur un problème de Gelfond : la somme des chiffres des nombres premiers, preprint.