Fractal tiles associated to generalised radix representations and shift
radix systems
Paul Surer
University Leoben, Austria
For
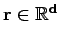 define the mapping
define the mapping
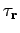 is called a shift radix system (SRS) if
is called a shift radix system (SRS) if
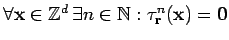 .
Shift radix systems are a class of dynamical systems,
introduced in 2005 by Akiyama et al., and
are strongly related to other well known notions of number systems as
.
Shift radix systems are a class of dynamical systems,
introduced in 2005 by Akiyama et al., and
are strongly related to other well known notions of number systems as
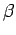 -expansion or canonical number systems. Let
Further denote by
-expansion or canonical number systems. Let
Further denote by
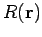 the companion matrix with the characteristic
polynomial
the companion matrix with the characteristic
polynomial
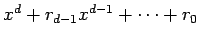 .
For
.
For
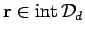 ,
,
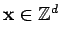 define
and
(using the limit with respect to a Hausdorff metric).
Then
define
and
(using the limit with respect to a Hausdorff metric).
Then
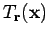 is called an SRS-tile. We will give
basic properties of such tiles and see, how they are related to tiles induced
by Pisot numbers and canonical number systems.
is called an SRS-tile. We will give
basic properties of such tiles and see, how they are related to tiles induced
by Pisot numbers and canonical number systems.
Supported by FWF Project Nr. P9610-N13.
![]() define the mapping
define the mapping
