On some distribution related to digital expansions
Ligia-Loretta Cristea
Johannes Kepler Universität Linz, Austria
Coauthor(s): Helmut Prodinger
All results presented here stem from joint work with Helmut Prodinger.
First, we study certain probability measures of binomial type defined in a
recursive way on the unit interval. These measures are related to the
sum-of-digit function and similar quantities. In particular, we undertake an
asymptotic analysis of the moments of the corresponding distributions.
Subsequently, we consider certain aspects of the Cantor-Fibonacci distribution.
The Cantor distribution is a probability distribution whose cumulative
distribution function is the Cantor function. It is obtained from strings
consisting of letters 0 and 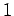 and appropriately attaching a value to them. The Cantor-Fibonacci distribution
additionally rejects strings with two adjacent letters
and appropriately attaching a value to them. The Cantor-Fibonacci distribution
additionally rejects strings with two adjacent letters 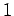 . A probability model
is associated by assuming that each admissible string (word) of length
. A probability model
is associated by assuming that each admissible string (word) of length 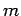 is
equally likely; eventually the limit
is
equally likely; eventually the limit
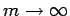 is considered.
is considered.
We assume that 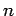 random numbers (values of random strings) are drawn
independently. We study order statistics of these
random numbers (values of random strings) are drawn
independently. We study order statistics of these 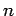 values: the (average of)
the smallest resp. largest of them.
values: the (average of)
the smallest resp. largest of them.
Supported by the Austrian Science Foundation (FWF), project S9609,
``Analytic and Probabilistic Methods in Combinatorics''.