
The (SFB) Combinatorics Afternoon Workshop will take place on 6 June 2025 (Friday) in the afternoon at the seminar room STEG050 (AE06) on the ground floor (EG) of the Mathematics Building located at Steyrergasse 30, A-8010 Graz, on the Neue Technik Campus of TU Graz.
Michael Krivelevich (Tel Aviv University): Percolation through isoperimetry
Let G be a d-regular graph of growing degree on n vertices, and form a random subgraph G_p of G by retaining each edge of G independently with probability p=p(d). Which conditions on G suffice to observe a phase transition at p=1/d similar to that in the binomial random graph G(d+1,p), or, say, in a random subgraph of the binary hypercube Q^d? We argue that in the supercritical regime p=(1+ε)/d, ε>0 being a small constant, postulating that every vertex subset S of G of at most n/2 vertices has its edge boundary at least C|S|, for some large enough constant C=C(ε)>0, suffices to guarantee the likely appearance of the giant component in G_p. Moreover, its asymptotic order is equal to that in the random graph G(n,(1+ε)/n), and all other components are typically much smaller. We further give examples demonstrating the tightness of this result in several key senses. A joint work with Sahar Diskin, Joshua Erde and Mihyun Kang.

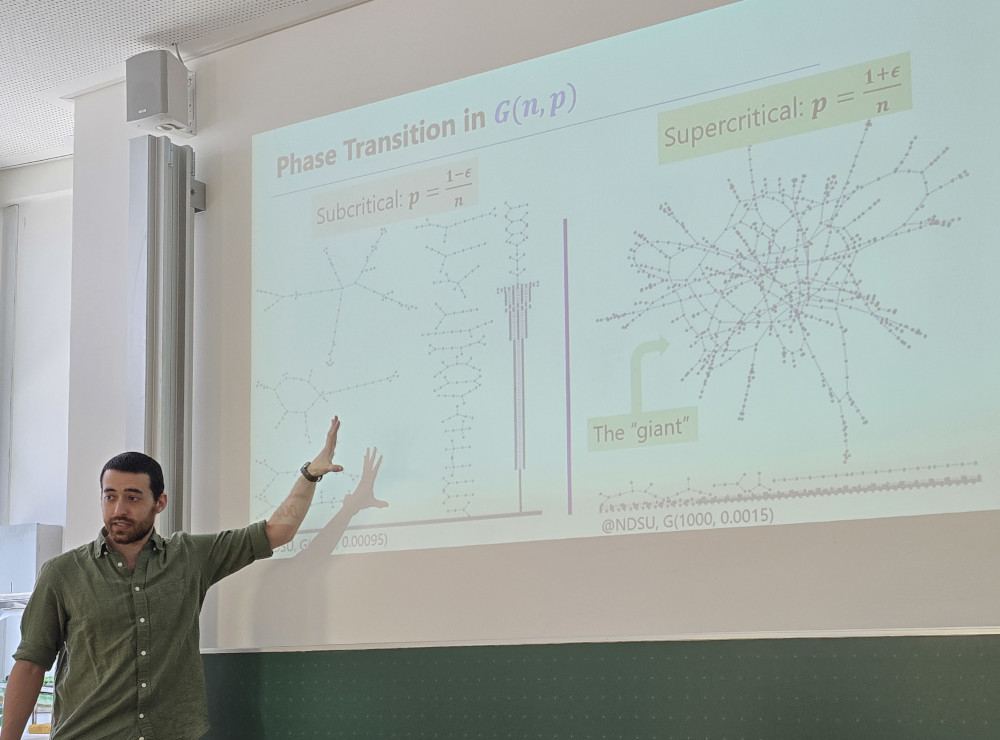
Sahar Diskin (Tel Aviv University): Universality of the Erdős-Rényi component phenomena
A classical result by Erdős and Rényi from 1960 shows that the binomial random graph G(n,p) undergoes a fundamental phase transition in its component structure when the expected average degree is around 1 (i.e., around p=1/n). Specifically, for p = (1-ε)/n, where ε>0 is a constant, all connected components are typically logarithmic in n, whereas for p = (1+ε)/n a unique giant component of linear order emerges, and all other components are of order at most logarithmic in n. A similar phenomenon — the typical emergence of a unique giant component surrounded by components of at most logarithmic order — has been observed in random subgraphs G_p of specific host graphs G, such as the d-dimensional binary hypercube, random d-regular graphs, and pseudo-random (n,d,λ)graphs, though with quite different proofs. This naturally leads to the question: What assumptions on a d-regular n-vertex graph G suffice for its random subgraph to typically exhibit this phase transition around the critical probability p=1/(d-1)? Furthermore, is there a unified approach that encompasses these classical cases? In this talk, we demonstrate that it suffices for G to have mild global edge expansion and (almost-optimal) expansion of sets of (poly-)logarithmic order in n. This result covers many previously considered concrete setups. We also discuss the tightness of our sufficient conditions. Joint work with Michael Krivelevich.
Michael Anastos (IST Austria): Nearly spanning cycle in the percolated hypercube
Let Q^d be the d-dimensional binary hypercube. We form a random subgraph Q^d_p of Q^d by retaining each edge of Q^d independently with probability p=p(d). We show that, for every constant ε>0, there exists a constant C=C(ε)>0 such that, if p ≥ C/d, then with high probability Q^d_p contains a cycle of length at least (1-ε)2^d. This confirms a long-standing folklore conjecture. A joint work with Sahar Diskin, Joshua Erde, Mihyun Kang, Michael Krivelevich and Lyuben Lichev.

(SFB) Combinatorics Afternoon Workshop is an associated event of the SFB "Discrete random structures: enumeration and scaling limits". It is supported in part by Austrian Science Fund (FWF) [10.55776/F1002] and [10.55776/DOC183].