Differentialgleichungen am Computer

Lösungen von Differentialgleichungen

Differentialgleichungen 1. Ordnung:

> eq1:=diff(y(t),t)=k*y(t);

> sol1:=dsolve(eq1,y(t));

Anfangswertproblem: y(0)=2

> eval(subs(t=0, y(0)=2, sol1));

> subs(_C2=2, sol1);

oder einfacher lösen wir die Diffe

rentialgleichung gleich als Anfangswertproblem

> sol1b:=dsolve({eq1, y(0)=2}, y(t));

Setzen wir k=-0.5 und lassen wir die Lösungskurve zeichnen:

> sol1c:=subs(k=-0.5, sol1b);

> plot(sol1c, t=0..3);

rhs ... 'right hand side'

Plotting error, empty plot

> plot(rhs(sol1c), t=0..3);

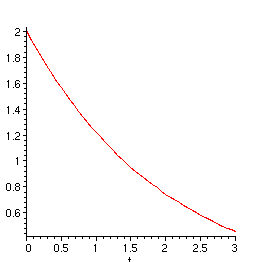
Zur Kontrolle, ob eine zum Bsp. von Hand gerechneten Lösung wirklich Lösung der Differentialgleichung ist:

> eq2:=diff(y(x), x)=1+y(x)^2;

> y2:=tan(x+c);

> subs(y(x)=y2, eq2);

> eval(%);

Differentialgleichungen 2. Ordnung:

Dgl. 2. Ordnung mit konstanten Koeffizienten und lamda1 = lamda2

> eq3:=(D@@2)(y)(x)+3*D(y)(x)+9/4*y(x)=0;

> yp3:=dsolve({eq3,y(0)=1, D(y)(0)=-2},y(x));

> plot(rhs(yp3), x=0..5, y=-0.1..0.1);

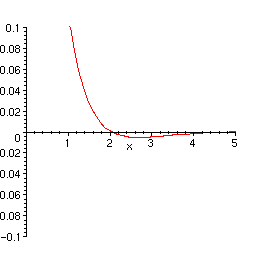
Charakteristische Gleichung besitzt konjugiert komplexe Lösungen

> eq4:=(D@@2)(y)(x)+2*D(y)(x)+2501*y(x)=0;

> yp4:=dsolve({eq4, y(0)=1, D(y)(0)=-1}, y(x));

> plot(rhs(yp4), x=0..2,numpoints=1000);

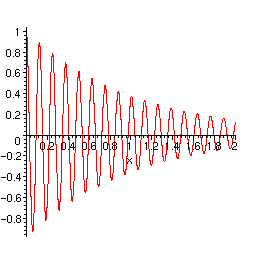
Eulersche Dgl.: Charakteristische Gleichung besitzt konjugiert komplexe Lösungen (0.10)

> eq5:=x^2*(D@@2)(y)(x)+x*D(y)(x)+y(x)=0;

> yp5:=dsolve({eq5, y(1)=0, D(y)(1)=1}, y(x));

> plot(rhs(yp5), x=0..10);

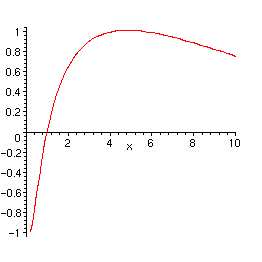
Zur Kontrolle, ob eine zum Bsp. von Hand gerechneten Lösung wirklich Lösung der Differentialgleichung ist: (0.1b)

> eq6:=(1-x)*diff(y(x), x,x)+x*diff(y(x),x)-y(x)=0;

> y6:=exp(x)+x;

> subs(y(x)=y6, eq6);

> simplify(eval(%));

Inhomogene Dgl:

> Ly7:=diff(y(x),x,x)-4*diff(y(x),x)+3*y(x);

> g7:=10*exp(-2*x);

> sol7:=dsolve({Ly7=g7,y(0)=1, D(y)(0)=-3},y(x));

Lineare Dgln. höherer Ordnung:

Wronskideterminante:

> eq8:=(D@@4)(y)(x)-5*(D@@2)(y)(x) + 4*y(x)=0;

> dsolve(eq8, y(x));

Basis von Lösungen:

> with(linalg):

> B8:=[exp(x), exp(2*x), exp(-2*x), exp(-x)];

Warning, new definition for norm

Warning, new definition for trace

> A8:=matrix([B8, diff(B8,x), diff(B8,x,x), diff(B8,x,x,x)]);

> W:=det(A8);

> W:=simplify(%);

Systeme von Differentialgleichungen:

> sys1:=D(z1)(t)=-3*z1(t)+z2(t),D(z2)(t)=z1(t)-3*z2(t);

> dsolve({sys1}, {z1(t), z2(t)});

> dsolve({sys1, z1(0)=1, z2(0)=5}, {z1(t), z2(t)});

> with(linalg):

> A1:=matrix(2,2,[-3,1,1,-3]);

> eigA1:=eigenvects(A1);

> lamda1:=eigA1[1][1];

> x11:=eigA1[1][3][1];

> lamda2:=eigA1[2][1];

> x12:=eigA1[2][3][1];

> sol1:=_C1*x11*exp(lamda1*t)+_C2*x12*exp(lamda2*t);

> sol1:=evalm(%);

>

Phasenportraits

Phasenportäts:

> with(share); with(ODE);

Share Library:  ODE

Author: Daniel Schwalbe.

Description:  package for solving ODE's numerically and plottingtheir solutions

uneigentlicher Knoten im Ursprung:

> eq1:=(t,y1,y2) ->-3*y1+y2;

> eq2:=(t,y1,y2) ->y1-3*y2;

> inits:=[1,1],[-1,1],[-1,-1],[1,-1],[1,3],[-3,-1],[-1,-3],[3,1],[0,2],[-2,0],[0,-2],[2,0]:

> phaseplot([eq1,eq2],-3..3,-2..2,{inits},numsteps=200);

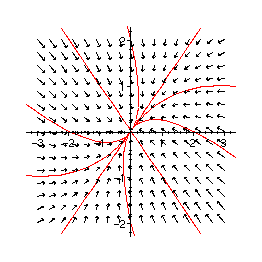
Sattelpunkt:

> sys2:=D(y1)(t)=2*y1(t)-4*y2(t),D(y2)(t)=y1(t)-3*y2(t);

> sol2:=dsolve({sys2},{y1(t),y2(t)});

>

> eq21:=(t,y1,y2) ->2*y1-4*y2;

> eq22:=(t,y1,y2) ->y1-3*y2;

> inits:=[1,1],[-1,-1],[4,1],[-4,-1],[0,1],[0,-1],[0,2],[0,-2],[2,1],[-2,-1],[3,2],[-3,-2];

> phaseplot([eq21,eq22], -5..5, -4..4, {inits}, numsteps=200);

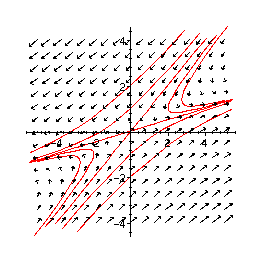
'Center'

> sys3:=D(y1)(t)=y2(t), D(y2)(t)=-4*y1(t);

> sol3:=dsolve({sys3},{y1(t),y2(t)});

> eq31:=(t,y1,y2) -> y2;

> eq32:=(t,y1,y2) -> -4*y1;

> inits:=[0,1], [0,2], [0,3];

> phaseplot([eq31,eq32], -6..6, -4..4, {inits}, numsteps=200);

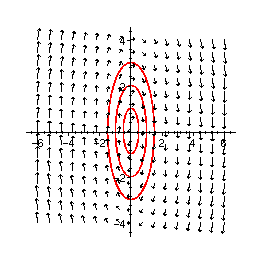
Strudelpunkt:

> sys4:=D(y1)(t)=-y1(t)+y2(t), D(y2)(t)=-y1(t)-y2(t);

> sol4:=dsolve({sys4},{y1(t),y2(t)});

>

> eq41:=(t,y1,y2) ->-y1+y2;

> eq42:=(t,y1,y2) ->-y1-y2;

> inits1:=[1,0],[2,0],[3,0],[-1,0],[-2,0],[-3,0];

> phaseplot([eq41,eq42], -5..5, -4..4, {inits1}, numsteps=200);

> inits2:=[0,1],[0,2],[0,3],[0,-1],[0,-2],[0,-3];

> phaseplot([eq41,eq42], -5..5, -4..4, {inits2}, numsteps=200);

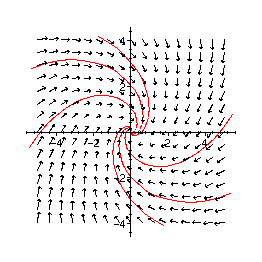
> eq51:=(t,y1,y2) -> y2;

> eq52:=(t,y1,y2) -> -sin(y1);

> inits:=[0,1/2],[0,1],[0,3/2],[0,2],[0,5/2],[0,3],[0,4],[0,-5/2],[0,-3],[0,-4],[2*Pi,1/2],[2*Pi,1],[2*Pi,3/2],[2*Pi,2];

> phaseplot([eq51,eq52], -Pi..3*Pi, -4..4, {inits}, numsteps=200);

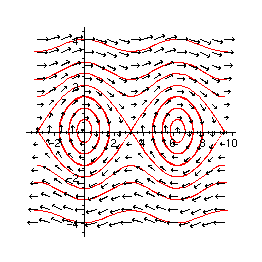
Damping

> eq61:=(t,y1,y2) -> y2;

> eq62:=(t,y1,y2) -> -sin(y1)-1/2*y2;

> inits:=[0,1/2],[0,1],[0,3/2],[0,2],[0,5/2],[0,3],[0,4],[0,-1],[0,-3/2],[0,-2],[2*Pi,1/2],[2*Pi,-1],[2*Pi,-3/2];

> phaseplot([eq61,eq62], -Pi..3*Pi, -4..4, {inits}, numsteps=200);

>

>

>

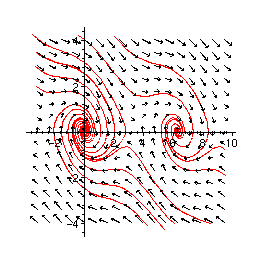
Potenzreihenansätze

Potenzreihen:

> series(exp(x),x);

> series (ln(1+x),x,10);

Entwicklungsmitte Pi/2

> f:=series(sin(x),x=Pi/2,8);

Um Graphen zu zeichnen ist es nötig zuerst den Fehlerterm O(x^n) zu eliminieren

> p:=convert(f,polynom);

> plot(p,x=-2*Pi..2*Pi,y=-2..2);

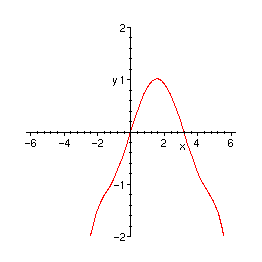
> f:=series(sin(x),x=Pi/2,64):

> p:=convert(f,polynom):

> plot(p,x=-5*Pi..5*Pi,y=-1..1);

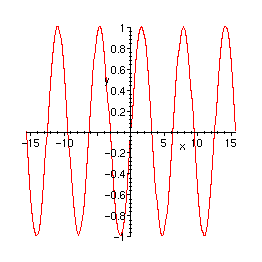
Lösen von Differentialgleichungen mittels Potenzreihenansatz:

> eq1:=D(y)(x)+2*x*y(x)=0;

> dsolve(eq1, y(x), series);

Für ein Anfangswertproblem:

> dsolve({eq1, y(0)=1}, y(x), series);

> Order:=12;

> sol1:=dsolve(eq1,y(x),series);

> yp1:=subs(y(0)=1, sol1);

> yp1:=convert(rhs(yp1),polynom);

> plot(yp1,x=-1..1);

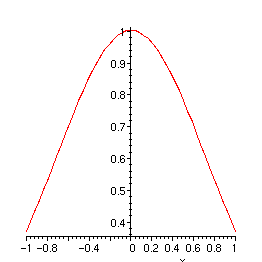
Orthogonale Polynome:

Legendre Polynome:

> with(orthopoly);

P(n,x) erzeugt das n-te Legendre Polynom:

> P(2,x);

> P(3,x);

> P(4,x);

Oder wir schreiben eine eigene Prozedur, um diese Polynome zu erzeugen

> Legendre:=proc(n)

> if n=0

> then 1

> else 1/(2^n*n!)*diff((x^2-1)^n,x$n)

> fi;

> end:

> Legendre(2);

> Legendre(3);

> simplify(%);

> S:=seq(simplify(Legendre(n)), n=0..4);

> plot({S}, x=-1.5..1.5, y=-1..1);

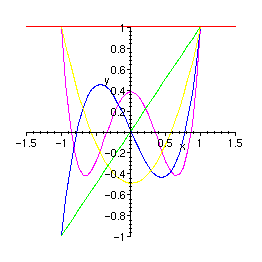
> S:=seq(simplify(Legendre(n)), n=10..15);

> plot({S}, x=-1.5..1.5, y=-1..1,numpoints=1500);

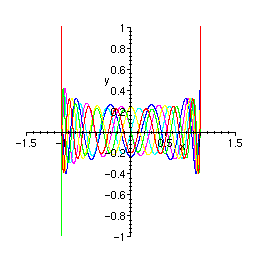
> eq2:=(1-x^2)*(D@@2)(y)(x)-2*x*D(y)(x)+6*y(x)=0;

> P2:=dsolve({eq2, y(-1)=1,y(1)=1},y(x));

> eq3:=(1-x^2)*(D@@2)(y)(x)-2*x*D(y)(x)+12*y(x)=0;

> P3:=dsolve({eq3,y(-1)=-1,y(1)=1},y(x));

Bessel Funktion:

> J0:=series(BesselJ(0,x),x=0,11);

> J0:=convert(J0,polynom);

> plot(J0,x=0..6,y=-1..1);

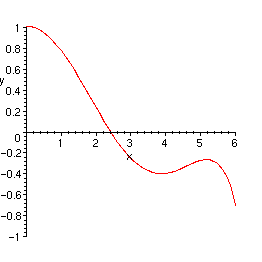
> plot({BesselJ(0,x),BesselJ(1,x)},x=0..12);

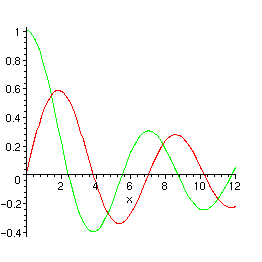
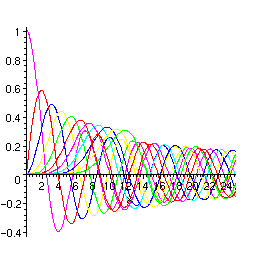
> S:=seq(BesselJ(n,x), n=0..10);

> plot({S}, x=0..25);

> eq4:=x*(D@@2)(y)(x)+D(y)(x)+x*y(x)=0;

> Order:=11;

> dsolve({eq4,y(0)=1,D(y)(0)=0},y(x),series);

> evalf(%);

>

>