Computermathematik (für Informatik)

2. Übungsblatt (Musterlösung)
5. 11. 2008

Die heutigen Übungen sollen mit dem Computeralgebrasystem Sage gelöst werden.

Die Lösung der Beispiele soll auf möglichst kompakte Weise erfolgen. Wenn zum Beispiel eine Funktion für mehrere Werte berechnet werden soll, soll das mittels einer geeigneten Schleifen oder Listen Operation erfolgen, und nicht alle Werte einzeln eingetippt werden.

Zwischenergebnisse welche in einem weiteren Berechnungsschritt benötigt werden, sollen in eine Variable gespeichert und weiterverwendet werden (nicht neu eintippen).

Beispiel 11

Bestimmen Sie die Anzahl der Stellen, sowie die Summe der Ziffern von n! wobei n die Werte 1, 10, 100, 1000, 10000 und 100000 annimmt.

[factorial(10^i).ndigits() for i in [0..5]]

[1, 7, 158, 2568, 35660, 456574]

[1, 7, 158, 2568, 35660, 456574]

[sum(factorial(10^i).digits(base = 10)) for i in [0..5]]

[1, 27, 648, 10539, 149346, 1938780]

[1, 27, 648, 10539, 149346, 1938780]

show([[f.ndigits(), sum(f.digits(base = 10))] for f in [factorial(10^i) for i in [0..5]]])

\begin{array}{l}[\left[1, 
 1\right],\\
\left[7, 
 27\right],\\
\left[158, 
 648\right],\\
\left[2568, 
 10539\right],\\
\left[35660, 
 149346\right],\\
\left[456574, 
 1938780\right]]\end{array}

\begin{array}{l}[\left[1, 
 1\right],\\
\left[7, 
 27\right],\\
\left[158, 
 648\right],\\
\left[2568, 
 10539\right],\\
\left[35660, 
 149346\right],\\
\left[456574, 
 1938780\right]]\end{array}

Beispiel 12

Untersuchen Sie, für welche n \leq 30 die Primfaktorzerlegung von f(n)=n!-1 Primfaktoren mehrfach enthält. Geben sie eine Liste dieser Zahlen und ihrer Primfaktorzerlegungen aus.

def f(n):
return factorial(n) - 1

show([[n, f(n), factor(f(n))] for n in [1..30] if squarefree_part(f(n)) != f(n)])

\begin{array}{l}[\left[9, 
 362879, 
 11^{2} \cdot 2999\right],\\
\left[15, 
 1307674367999, 
 17 \cdot 31^{2} \cdot 53 \cdot 1510259\right]]\end{array}

\begin{array}{l}[\left[9, 
 362879, 
 11^{2} \cdot 2999\right],\\
\left[15, 
 1307674367999, 
 17 \cdot 31^{2} \cdot 53 \cdot 1510259\right]]\end{array}

squareList=[]

for n in [2..30]:
fact = factor(f(n))
for (primfactor, mult) in fact:
if (mult>1):
squareList.append([n, f(n), fact])
break

show(squareList)

\begin{array}{l}[\left[9, 
 362879, 
 11^{2} \cdot 2999\right],\\
\left[15, 
 1307674367999, 
 17 \cdot 31^{2} \cdot 53 \cdot 1510259\right]]\end{array}

\begin{array}{l}[\left[9, 
 362879, 
 11^{2} \cdot 2999\right],\\
\left[15, 
 1307674367999, 
 17 \cdot 31^{2} \cdot 53 \cdot 1510259\right]]\end{array}

Beispiel 13

Eine Zahl M_p = 2^p-1 ist höchstens dann eine Primzahl wenn p selbst prim ist. Primzahlen dieser Form nennt man Mersennesche Primzahlen.Die größten bekannten Primzahlen haben diese Form. Es ist unbekannt, ob es unendlich viele Mersennesche Primzahlen gibt.
Bestimmen Sie für p\leq 500 alle Mersenneschen Primzahlen. Geben Sie Ihr Ergebnis als Tabelle mit den Spalten p und M_p an.

show([[p, 2^p - 1] for p in [1..500] if is_prime(p) and is_prime(2^p - 1)])

\begin{array}{l}[\left[2, 
 3\right],\\
\left[3, 
 7\right],\\
\left[5, 
 31\right],\\
\left[7, 
 127\right],\\
\left[13, 
 8191\right],\\
\left[17, 
 131071\right],\\
\left[19, 
 524287\right],\\
\left[31, 
 2147483647\right],\\
\left[61, 
 2305843009213693951\right],\\
\left[89, 
 618970019642690137449562111\right],\\
\left[107, 
 162259276829213363391578010288127\right],\\
\left[127, 
 170141183460469231731687303715884105727\right]]\end{array}

\begin{array}{l}[\left[2, 
 3\right],\\
\left[3, 
 7\right],\\
\left[5, 
 31\right],\\
\left[7, 
 127\right],\\
\left[13, 
 8191\right],\\
\left[17, 
 131071\right],\\
\left[19, 
 524287\right],\\
\left[31, 
 2147483647\right],\\
\left[61, 
 2305843009213693951\right],\\
\left[89, 
 618970019642690137449562111\right],\\
\left[107, 
 162259276829213363391578010288127\right],\\
\left[127, 
 170141183460469231731687303715884105727\right]]\end{array}

Beispiel 14

Finden Sie heraus wie man Grenzwerte mit Sage berechnet.

Berechnen Sie die Grenzwerte:

(a) \displaystyle \quad\lim_{x\to-\infty} \arctan\left(e^{-x}\right)

var('x')
show(limit(arctan(e^(-x)), x=-oo))

\frac{\pi}{2}

\frac{\pi}{2}

(b) \displaystyle \quad\lim_{x\to\infty} \frac{\sqrt{9 x^2 + 10}}{12 x + 1}

show(limit(sqrt(9*x^2+10)/(12*x+1),x=oo))

\frac{1}{4}

\frac{1}{4}

var('x c')
assume(c > 0)
limit(1/(sqrt(x + 1) * (sqrt(x^2 + c) - sqrt(x^2 - c) + 1)), x=oo)

Beispiel 15

Lösen Sie die Gleichung

\frac{(2i + 1)z + 9}{(4i + 3)z - 4i - 9} = 8 - 5i

über den Komplexen Zahlen. Berechnen Sie den Real- und Imaginärteil der Lösung. Und testen Sie, durch Einsetzen in die Gleichung ob die Lösung korrekt ist.

var('z')

eqn = ((2*I + 1)*z + 9)/((4*I + 3)*z - 4*I - 9) == 8 - 5*I
show(eqn)

\frac{{\left( {2 i} + 1 \right) z} + 9}{{\left( {4 i} + 3 \right) z} - {4 i} - 9}  =  8 - {5 i}

\frac{{\left( {2 i} + 1 \right) z} + 9}{{\left( {4 i} + 3 \right) z} - {4 i} - 9}  =  8 - {5 i}

zsol = solve(eqn,z)[0]
show(zsol)

z  =  \frac{101 - {13 i}}{{15 i} + 43}

z  =  \frac{101 - {13 i}}{{15 i} + 43}

z1 = zsol.right().real() + I * zsol.right().imag()
show(z1)

2 - i

2 - i

bool(eqn.subs(z = z1))

True

True

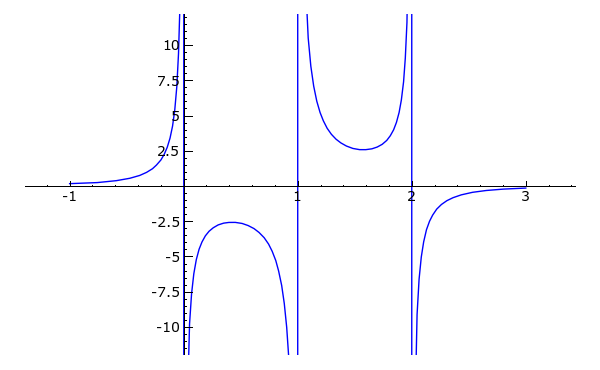
Beispiel 16

Berechnen Sie das Integral

\int\frac{3 x^2-6 x+2}{x^2 (x-1)^2 (x-2)^2} dx,

und zeichnen Sie den Graphen der Stammfunktion im Intervall [-1,3].

var('x')
f = (3 * x^2 - 6 * x + 2) / (x^2 * (x - 1)^2 * (x - 2)^2)
f.show()

\frac{{3 {x}^{2} } - {6 x} + 2}{{{{\left( x - 2 \right)}^{2}  {\left( x - 1 \right)}^{2} } {x}^{2} }}

\frac{{3 {x}^{2} } - {6 x} + 2}{{{{\left( x - 2 \right)}^{2}  {\left( x - 1 \right)}^{2} } {x}^{2} }}

fint = integrate(f, x).factor()
fint.show()

\frac{-1}{{{\left( x - 2 \right) \left( x - 1 \right)} x}}

\frac{-1}{{{\left( x - 2 \right) \left( x - 1 \right)} x}}

plot(f, x, -1, 3).show(ymin = -10, ymax = 10)

plot(fint, x, -1, 3).show(ymin = -10, ymax = 10)

Beispiel 17

Lösen Sie das Gleichungssystem

\begin{align*} x+y-z &= 6\\ x^2+y^2+z^2 &= 14\\ x^3+y^3-z^3 &= 36 \end{align*}

und überprüfen die jeweiligen Lösungen durch Einsetzen.

Berechnen Sie den Ausdruck x+2y+3z für alle Lösungen.

var('x y z')
eqn = [x + y - z == 6,
x^2 + y^2 + z^2 == 14,
x^3 + y^3 - z^3 == 36]

for i in eqn:
view(i)

-z + y + x  =  6
{z}^{2}  + {y}^{2}  + {x}^{2}   =  14
-{z}^{3}  + {y}^{3}  + {x}^{3}   =  36

-z + y + x  =  6
{z}^{2}  + {y}^{2}  + {x}^{2}   =  14
-{z}^{3}  + {y}^{3}  + {x}^{3}   =  36

sol = solve(eqn, [x, y, z], solution_dict = True)

for s in sol:
print s

{y: 3, x: 1, z: -2}
{y: 2, x: 1, z: -3}
{y: 3, x: 2, z: -1}
{y: 1, x: 2, z: -3}
{y: 1, x: 3, z: -2}
{y: 2, x: 3, z: -1}

{y: 3, x: 1, z: -2}
{y: 2, x: 1, z: -3}
{y: 3, x: 2, z: -1}
{y: 1, x: 2, z: -3}
{y: 1, x: 3, z: -2}
{y: 2, x: 3, z: -1}

show([[e(s) for e in eqn] for s in sol])

\begin{array}{l}[\left[6  =  6, 
 14  =  14, 
 36  =  36\right],\\
\left[6  =  6, 
 14  =  14, 
 36  =  36\right],\\
\left[6  =  6, 
 14  =  14, 
 36  =  36\right],\\
\left[6  =  6, 
 14  =  14, 
 36  =  36\right],\\
\left[6  =  6, 
 14  =  14, 
 36  =  36\right],\\
\left[6  =  6, 
 14  =  14, 
 36  =  36\right]]\end{array}

\begin{array}{l}[\left[6  =  6, 
 14  =  14, 
 36  =  36\right],\\
\left[6  =  6, 
 14  =  14, 
 36  =  36\right],\\
\left[6  =  6, 
 14  =  14, 
 36  =  36\right],\\
\left[6  =  6, 
 14  =  14, 
 36  =  36\right],\\
\left[6  =  6, 
 14  =  14, 
 36  =  36\right],\\
\left[6  =  6, 
 14  =  14, 
 36  =  36\right]]\end{array}

reduce(lambda x,y: x and y, flatten([[bool(e(s)) for e in eqn] for s in sol]))

True

True

expr = x + 2 * y + 3 * z
show(expr)

{3 z} + {2 y} + x

{3 z} + {2 y} + x

[expr(s) for s in sol]

[1, -4, 5, -5, -1, 4]

[1, -4, 5, -5, -1, 4]

Beispiel 18

Bestimmen Sie ein Polynom p(x) vom Grad 3, für das gilt:

p(-1) = -4 \quad p'(-1) = 13 \quad p(1) = 2 \quad p'(1) = 5

var('a, b, c, d')

(a, b, c, d)

(a, b, c, d)

p(x) = a * x^3 + b * x^2 + c * x + d
show(p)

x \ {\mapsto}\ {a {x}^{3} } + {b {x}^{2} } + {c x} + d

x \ {\mapsto}\ {a {x}^{3} } + {b {x}^{2} } + {c x} + d

p1(x) = diff(p, x)
show(p1)

x \ {\mapsto}\ {{3 a} {x}^{2} } + {{2 b} x} + c

x \ {\mapsto}\ {{3 a} {x}^{2} } + {{2 b} x} + c

eqns = [p(-1) == -4, p1(-1) == 13, p(1) == 2, p1(1) == 5]
show(eqns)

\begin{array}{l}[d - c + b - a  =  -4,\\
c - {2 b} + {3 a}  =  13,\\
d + c + b + a  =  2,\\
c + {2 b} + {3 a}  =  5]\end{array}

\begin{array}{l}[d - c + b - a  =  -4,\\
c - {2 b} + {3 a}  =  13,\\
d + c + b + a  =  2,\\
c + {2 b} + {3 a}  =  5]\end{array}

solution = solve(eqns, [a, b, c, d], solution_dict = True)
solution

[{a: 3, c: 0, b: -2, d: 1}]

[{a: 3, c: 0, b: -2, d: 1}]

psol(x) = p(x)(solution[0])
show(psol)

x \ {\mapsto}\ {3 {x}^{3} } - {2 {x}^{2} } + 1

x \ {\mapsto}\ {3 {x}^{3} } - {2 {x}^{2} } + 1

plot0 = list_plot([(-1, -4), (-1, 13), (1, 2), (1, 5)], rgbcolor = (0, 0, 0), pointsize = 15)
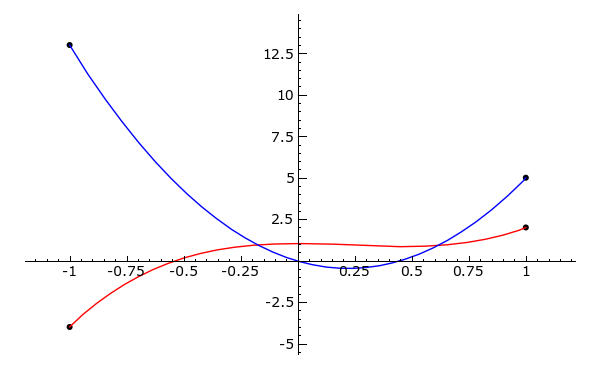
plot1 = plot(psol, -1, 1, color = "red")
plot2 = plot(diff(psol), -1, 1)
plot0 + plot1 + plot2

Beispiel 19

Beweisen Sie die folgenden trigonometrischen Identitäten durch Umformungen in Sage.

(a) \displaystyle \quad \sin(4x) + \cos(4x)\cot(2x) = \frac{1-\tan^2(x)}{2\tan(x)}

expr_a1 = sin(4 * x) + cos(4 * x) * cot(2 * x)
expr_a2 = (1 - tan(x)^2) / (2 * tan(x))
show(expr_a1 == expr_a2)

\sin \left( {4 x} \right) + {\cot \left( {2 x} \right) \cos \left( {4 x} \right)}  =  \frac{1 - {\tan \left( x \right)}^{2} }{{2 \tan \left( x \right)}}

\sin \left( {4 x} \right) + {\cot \left( {2 x} \right) \cos \left( {4 x} \right)}  =  \frac{1 - {\tan \left( x \right)}^{2} }{{2 \tan \left( x \right)}}

show(expr_a1.simplify_trig())
show(expr_a2.simplify_trig())

\frac{{2 {\cos \left( x \right)}^{2} } - 1}{{{2 \cos \left( x \right)} \sin \left( x \right)}}
\frac{{2 {\cos \left( x \right)}^{2} } - 1}{{{2 \cos \left( x \right)} \sin \left( x \right)}}

\frac{{2 {\cos \left( x \right)}^{2} } - 1}{{{2 \cos \left( x \right)} \sin \left( x \right)}}
\frac{{2 {\cos \left( x \right)}^{2} } - 1}{{{2 \cos \left( x \right)} \sin \left( x \right)}}

(expr_a1 / expr_a2).simplify_full()

(expr_a1 - expr_a2).simplify_full()

bool(expr_a1 == expr_a2)

True

True

(b) \displaystyle \quad \tan(3x) = \tan(x) \tan\left(\frac{\pi}{3} + x\right) \tan\left(\frac{\pi}{3} - x\right)

expr_b1 = tan(3 * x)
expr_b2 = tan(x) * tan(pi/3 + x) * tan(pi/3 - x)
show(expr_b1 == expr_b2)

\tan \left( {3 x} \right)  =  {{-\tan \left( x \right) \tan \left( x - \frac{\pi}{3} \right)} \tan \left( x + \frac{\pi}{3} \right)}

\tan \left( {3 x} \right)  =  {{-\tan \left( x \right) \tan \left( x - \frac{\pi}{3} \right)} \tan \left( x + \frac{\pi}{3} \right)}

show(expr_b1.simplify_trig())
show(expr_b2.simplify_trig())

\frac{{\left( {4 {\cos \left( x \right)}^{2} } - 1 \right) \sin \left( x \right)}}{{4 {\cos \left( x \right)}^{3} } - {3 \cos \left( x \right)}}
\frac{{\left( {4 {\cos \left( x \right)}^{2} } - 1 \right) \sin \left( x \right)}}{{4 {\cos \left( x \right)}^{3} } - {3 \cos \left( x \right)}}

\frac{{\left( {4 {\cos \left( x \right)}^{2} } - 1 \right) \sin \left( x \right)}}{{4 {\cos \left( x \right)}^{3} } - {3 \cos \left( x \right)}}
\frac{{\left( {4 {\cos \left( x \right)}^{2} } - 1 \right) \sin \left( x \right)}}{{4 {\cos \left( x \right)}^{3} } - {3 \cos \left( x \right)}}

(expr_b1 / expr_b2).simplify_full()

(expr_b1 - expr_b2).simplify_full()

bool(expr_b1 == expr_b2)

True

True

var('a b c')
expr_c1 = sin(a)^2 + sin(b)^2 + sin(c)^2
expr_c2 = 2 * cos(a) * cos(b) * cos(c) + 2
show(expr_c1 == expr_c2)

{\sin \left( c \right)}^{2}  + {\sin \left( b \right)}^{2}  + {\sin \left( a \right)}^{2}   =  {{{2 \cos \left( a \right)} \cos \left( b \right)} \cos \left( c \right)} + 2

{\sin \left( c \right)}^{2}  + {\sin \left( b \right)}^{2}  + {\sin \left( a \right)}^{2}   =  {{{2 \cos \left( a \right)} \cos \left( b \right)} \cos \left( c \right)} + 2

show(expr_c1(a = pi - b - c).simplify_full())
show(expr_c2(a = pi - b - c).simplify_full())

{{{{2 \cos \left( b \right)} \sin \left( b \right)} \cos \left( c \right)} \sin \left( c \right)} - {{2 {\cos \left( b \right)}^{2} } {\cos \left( c \right)}^{2} } + 2
{{{{2 \cos \left( b \right)} \sin \left( b \right)} \cos \left( c \right)} \sin \left( c \right)} - {{2 {\cos \left( b \right)}^{2} } {\cos \left( c \right)}^{2} } + 2

{{{{2 \cos \left( b \right)} \sin \left( b \right)} \cos \left( c \right)} \sin \left( c \right)} - {{2 {\cos \left( b \right)}^{2} } {\cos \left( c \right)}^{2} } + 2
{{{{2 \cos \left( b \right)} \sin \left( b \right)} \cos \left( c \right)} \sin \left( c \right)} - {{2 {\cos \left( b \right)}^{2} } {\cos \left( c \right)}^{2} } + 2

(expr_c1 / expr_c2)(a = pi - b - c).simplify_full()

(expr_c1 - expr_c2)(a = pi - b - c).simplify_full()

bool((expr_c1 == expr_c2)(a = pi - b - c))

True

True