Beispiel 20-27

Computermathematik (für Informatik)

3. Übungsblatt (Musterlösung)
19. 11. 2008

Die heutigen Übungen sollen mit dem Computeralgebrasystem Sage gelöst werden.

Die Lösung der Beispiele soll auf möglichst kompakte Weise erfolgen. Wenn zum Beispiel eine Funktion für mehrere Werte berechnet werden soll, soll das mittels einer geeigneten Schleifen oder Listen Operation erfolgen, und nicht alle Werte einzeln eingetippt werden.

Zwischenergebnisse welche in einem weiteren Berechnungsschritt benötigt werden, sollen in eine Variable gespeichert und weiterverwendet werden (nicht neu eintippen).

Beispiel 20

Bestimmen Sie den ganzzahligen Anteil und den Rest bei der Polynomdivision von:
\frac{x^8 + 2 x^7 - 3 x^5+2 x^4-x^3+x-3}{x^3-2 x^2-x-1}
P.<x> = QQ[] 
       
p1 = x^8 + 2*x^7 - 3*x^5 + 2*x^4 - x^3 + x - 3
p2 = x^3 - 2*x^2 - x - 1
show(p1/p2) 
        
\frac{x^{8} + 2 x^{7} - 3 x^{5} + 2 x^{4} - x^{3} + x - 3}{x^{3} - 2 x^{2} - x - 1}
\frac{x^{8} + 2 x^{7} - 3 x^{5} + 2 x^{4} - x^{3} + x - 3}{x^{3} - 2 x^{2} - x - 1}
p1 // p2 
        
x^5 + 4*x^4 + 9*x^3 + 20*x^2 + 55*x + 138
x^5 + 4*x^4 + 9*x^3 + 20*x^2 + 55*x + 138
p1 % p2 
        
351*x^2 + 194*x + 135
351*x^2 + 194*x + 135
g, r = p1.quo_rem(p2)
show(g)
show(r) 
        
x^{5} + 4 x^{4} + 9 x^{3} + 20 x^{2} + 55 x + 138


351 x^{2} + 194 x + 135
x^{5} + 4 x^{4} + 9 x^{3} + 20 x^{2} + 55 x + 138


351 x^{2} + 194 x + 135
show(g * p2 + r) 
        
x^{8} + 2 x^{7} - 3 x^{5} + 2 x^{4} - x^{3} + x - 3
x^{8} + 2 x^{7} - 3 x^{5} + 2 x^{4} - x^{3} + x - 3

Beispiel 21

Bestimmen Sie die Partialbruchdarstellung der folgenden rationalen Funktion:
\frac{2 x^5+11 x^4+3 x^3-19 x^2-16 x-12}{x^6 + 2 x^5 - 5 x^4 - 12 x^3 + 3 x^2 + 18 x + 9}
var('x') 
        
x
x
p3 = 2*x^5 + 11*x^4 + 3*x^3 - 19*x^2 - 16*x - 12
p4 = x^6 + 2*x^5 - 5*x^4 - 12*x^3 + 3*x^2 + 18*x + 9
show(p3 / p4) 
        
\frac{{2 {x}^{5} } + {11 {x}^{4} } + {3 {x}^{3} } - {19 {x}^{2} } - {16 x} - 12}{{x}^{6}  + {2 {x}^{5} } - {5 {x}^{4} } - {12 {x}^{3} } + {3 {x}^{2} } + {18 x} + 9}
\frac{{2 {x}^{5} } + {11 {x}^{4} } + {3 {x}^{3} } - {19 {x}^{2} } - {16 x} - 12}{{x}^{6}  + {2 {x}^{5} } - {5 {x}^{4} } - {12 {x}^{3} } + {3 {x}^{2} } + {18 x} + 9}
show((p3 / p4).partial_fraction()) 
        
\frac{-\left( {7 x} - 52 \right)}{{4 \left( {x}^{2}  - 3 \right)}} - \frac{{8 x} - 27}{{2 {\left( {x}^{2}  - 3 \right)}^{2} }} + \frac{15}{{4 \left( x + 1 \right)}} - \frac{9}{{4 {\left( x + 1 \right)}^{2} }}
\frac{-\left( {7 x} - 52 \right)}{{4 \left( {x}^{2}  - 3 \right)}} - \frac{{8 x} - 27}{{2 {\left( {x}^{2}  - 3 \right)}^{2} }} + \frac{15}{{4 \left( x + 1 \right)}} - \frac{9}{{4 {\left( x + 1 \right)}^{2} }}

Beispiel 22

Sei s(a) die jeweils größte reelle Lösung der Gleichung
x^5+x^4-x^3+x^2-x - a = 0.
Schreiben Sie eine Funktion die s(a) numerisch berechnet. Und zeichnen sie den Graphen der Funktion im Interval a\in[0, 100]. Hinweis: Verwenden Sie als Datentyp Polynome mit Koeffizienten in den rellen Zahlen.
P.<x> = RR[] 
       
polynom = x^5 + x^4 - x^3 + x^2 - x
show(polynom) 
        
1.00000000000000 x^{5} + 1.00000000000000 x^{4} - 1.00000000000000 x^{3} + 1.00000000000000 x^{2} - 1.00000000000000 x + 0.000000000000000
1.00000000000000 x^{5} + 1.00000000000000 x^{4} - 1.00000000000000 x^{3} + 1.00000000000000 x^{2} - 1.00000000000000 x + 0.000000000000000
def finde_groesste_nullstelle(a):
 p = polynom - a
 return max(p.roots(multiplicities = False)) 
       
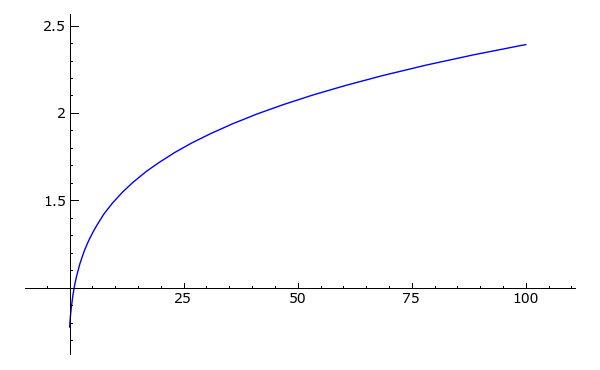plot(finde_groesste_nullstelle, (0, 100)) 
       

Beispiel 23

Bestimmen Sie symbolisch den Wert der unendlichen Reihe

\sum_{n=1}^\infty \frac{2^n (n!)^2}{(2n)!},
und überprüfen sie numerisch ob die Lösung korrekt sein kann.

Hinweis: Verwenden Sie das Maxima Interface von Sage, und den Maxima Befehl simplify_sum aus dem Maxima Paket simplify_sum.

maxima.load("simplify_sum") 
        
"/local/data/huss/software/sage-3.2.1/local/share/maxima/5.16.3/shar\
e/contrib/solve_rec/simplify_sum.mac"
"/local/data/huss/software/sage-3.2.1/local/share/maxima/5.16.3/share/contrib/solve_rec/simplify_sum.mac"
%maxima
s: sum((2^n*(n!)^2)/(2*n)!, n, 1, inf) 
        
'sum(2^n*n!^2/(2*n)!,n,1,inf)
'sum(2^n*n!^2/(2*n)!,n,1,inf)
show(maxima('s')) 
        
\sum_{n=1}^{\infty }{{{2^{n}\,n!^2}\over{\left(2\,n\right)!}}}
\sum_{n=1}^{\infty }{{{2^{n}\,n!^2}\over{\left(2\,n\right)!}}}
summe = maxima.simplify_sum('s').sage().expand()
show(summe) 
        
\frac{\pi}{2} + 1
\frac{\pi}{2} + 1
summe.n(digits = 100) 
        
2.570796326794896619231321691639751442098584699687552910487472296153\
90820314310449931401741267105853399
2.57079632679489661923132169163975144209858469968755291048747229615390820314310449931401741267105853399
def summe_numerisch(k):
 return sum([2^n*(factorial(n))^2/factorial(2*n) for n in [1..k]]) 
       
summe_numerisch(1000).n(digits = 100) 
        
2.570796326794896619231321691639751442098584699687552910487472296153\
908203143104499314017412671058534
2.570796326794896619231321691639751442098584699687552910487472296153908203143104499314017412671058534

Beispiel 24

Finden Sie eine geschlossene Formel für die Summe

\sum_{k=1}^n 3k^2 + 3k.
Beweisen Sie Ihre Formel durch vollständige Induktion. Die algebraischen Umformungen für diesen Beweis sollen natürlich auch mit Sage vorgenommen werden.

Hinweis: Verwenden Sie das Maxima Interface von Sage, und den Maxima Befehl simplify_sum aus dem Maxima Paket simplify_sum.

maxima.load("simplify_sum") 
        
"/local/data/huss/software/sage-3.2.1/local/share/maxima/5.16.3/shar\
e/contrib/solve_rec/simplify_sum.mac"
"/local/data/huss/software/sage-3.2.1/local/share/maxima/5.16.3/share/contrib/solve_rec/simplify_sum.mac"
var('k, n')
a = 3*k^2 + 3*k 
       
maxima("a: %s" % repr(a)) 
        
3*k^2+3*k
3*k^2+3*k
%maxima
s1: sum(a, k,1,n) 
        
'sum(3*k^2+3*k,k,1,n)
'sum(3*k^2+3*k,k,1,n)
show(maxima('s1')) 
        
\sum_{k=1}^{n}{3\,k^2+3\,k}
\sum_{k=1}^{n}{3\,k^2+3\,k}
sumexpr(n) = maxima.simplify_sum('s1').sage().factor()
show(sumexpr(n)) 
        
{{n \left( n + 1 \right)} \left( n + 2 \right)}
{{n \left( n + 1 \right)} \left( n + 2 \right)}
Induktionsbasis:
bool(sumexpr(1) == a(1)) 
        
True
True
Induktionsschritt:
bool(sumexpr(n+1).expand() == (sumexpr(n) + a(n+1)).expand()) 
        
True
True

Beispiel 25

Eine Partition einer Menge A ist eine Zerlegung A = B_1\cup B_2\cup\cdots\cup B_k in paarweise disjunkte, nichtleere Teilmengen B_j\subseteq A. Die Anzahl der verschiedenen Partitionen der Menge A = \lbrace 1,2,\ldots,n\rbrace in k nichtleere Teilmengen wird mit \begin{Bmatrix}n \\ k\end{Bmatrix} bezeichnet. Diese Zahlen heißen Stirlingsche Zahlen der 2. Art und sie erfüllen die Rekursion
\begin{Bmatrix} n \\ k \end{Bmatrix} = \begin{Bmatrix} n-1 \\ k-1\end{Bmatrix} + k\begin{Bmatrix}n-1 \\ k\end{Bmatrix}.
mit
  1. Schreiben Sie eine Funktion num_of_partitions(n, k) die \begin{Bmatrix}n \\ k\end{Bmatrix} berechnet. Und erstellen Sie eine Tabelle mit allen Werten der Stirling Zahlen 2. Art für n,k \leq 10.
  2. Berechnen Sie mit Ihrer Funktion \begin{Bmatrix}100 \\ 55 \end{Bmatrix} und vergleichen Sie Ihr Ergebnis mit der eingebauten Funktion stirling_number2
Direkte rekursive Implementation (Achtung: Hat exponentielle Laufzeit):
def num_of_partitions(n, k):
   if n == 0 and k == 0:
       return 1
   if n == 0 or k == 0:
       return 0
   if n > 0 and k > 0:    
       return num_of_partitions(n-1, k-1) + k * num_of_partitions(n-1, k)

   raise ValueError, "The number of Partitions is not defined for negative parameters" 
       
def print_table(f):
   for n in [0..10]:
       if n == 0:
           string = "n\k| "
           line   = "-----"
           for k in [0..10]:
               string += "%5d " % k
               line += 6 * "-"
           print string
           print line

       string = "%3d| " % n
       for k in [0..10]:
           string += "%5d " % f(n, k)
       print string 
       
print_table(num_of_partitions) 
        
n\k|     0     1     2     3     4     5     6     7     8     9    10
-----------------------------------------------------------------------
  0|     1     0     0     0     0     0     0     0     0     0     0
  1|     0     1     0     0     0     0     0     0     0     0     0
  2|     0     1     1     0     0     0     0     0     0     0     0
  3|     0     1     3     1     0     0     0     0     0     0     0
  4|     0     1     7     6     1     0     0     0     0     0     0
  5|     0     1    15    25    10     1     0     0     0     0     0
  6|     0     1    31    90    65    15     1     0     0     0     0
  7|     0     1    63   301   350   140    21     1     0     0     0
  8|     0     1   127   966  1701  1050   266    28     1     0     0
  9|     0     1   255  3025  7770  6951  2646   462    36     1     0
 10|     0     1   511  9330 34105 42525 22827  5880   750    45     1 
n\k|     0     1     2     3     4     5     6     7     8     9    10
-----------------------------------------------------------------------
  0|     1     0     0     0     0     0     0     0     0     0     0 
  1|     0     1     0     0     0     0     0     0     0     0     0 
  2|     0     1     1     0     0     0     0     0     0     0     0 
  3|     0     1     3     1     0     0     0     0     0     0     0 
  4|     0     1     7     6     1     0     0     0     0     0     0 
  5|     0     1    15    25    10     1     0     0     0     0     0 
  6|     0     1    31    90    65    15     1     0     0     0     0 
  7|     0     1    63   301   350   140    21     1     0     0     0 
  8|     0     1   127   966  1701  1050   266    28     1     0     0 
  9|     0     1   255  3025  7770  6951  2646   462    36     1     0 
 10|     0     1   511  9330 34105 42525 22827  5880   750    45     1
print_table(stirling_number2) 
        
n\k|     0     1     2     3     4     5     6     7     8     9    10
-----------------------------------------------------------------------
  0|     1     0     0     0     0     0     0     0     0     0     0
  1|     0     1     0     0     0     0     0     0     0     0     0
  2|     0     1     1     0     0     0     0     0     0     0     0
  3|     0     1     3     1     0     0     0     0     0     0     0
  4|     0     1     7     6     1     0     0     0     0     0     0
  5|     0     1    15    25    10     1     0     0     0     0     0
  6|     0     1    31    90    65    15     1     0     0     0     0
  7|     0     1    63   301   350   140    21     1     0     0     0
  8|     0     1   127   966  1701  1050   266    28     1     0     0
  9|     0     1   255  3025  7770  6951  2646   462    36     1     0
 10|     0     1   511  9330 34105 42525 22827  5880   750    45     1 
n\k|     0     1     2     3     4     5     6     7     8     9    10
-----------------------------------------------------------------------
  0|     1     0     0     0     0     0     0     0     0     0     0 
  1|     0     1     0     0     0     0     0     0     0     0     0 
  2|     0     1     1     0     0     0     0     0     0     0     0 
  3|     0     1     3     1     0     0     0     0     0     0     0 
  4|     0     1     7     6     1     0     0     0     0     0     0 
  5|     0     1    15    25    10     1     0     0     0     0     0 
  6|     0     1    31    90    65    15     1     0     0     0     0 
  7|     0     1    63   301   350   140    21     1     0     0     0 
  8|     0     1   127   966  1701  1050   266    28     1     0     0 
  9|     0     1   255  3025  7770  6951  2646   462    36     1     0 
 10|     0     1   511  9330 34105 42525 22827  5880   750    45     1
Rekursive Implementation mit Memoization (lineare Laufzeit, quadratischer Speicherbedarf):
partitions_cache = {}

def num_of_partitions(n, k):

   def num_of_partitions_local(n, k):
       if (n, k) not in partitions_cache:
           partitions_cache[(n, k)] = num_of_partitions(n, k)
       return partitions_cache[(n, k)]

   if n == 0 and k == 0:
       return 1
   if n == 0 or k == 0:
       return 0
   if n > 0 and k > 0:
       return num_of_partitions_local(n-1, k-1) + k * num_of_partitions_local(n-1, k)

   raise ValueError, "The number of Partitions is not defined for negative parameters" 
       
time num_of_partitions(100, 55) 
        
44754563535486898023760406147845887138100226753724037248460285587734\
0726924157920380127788644000
CPU time: 0.02 s,  Wall time: 0.03 s
447545635354868980237604061478458871381002267537240372484602855877340726924157920380127788644000
CPU time: 0.02 s,  Wall time: 0.03 s
time stirling_number2(100, 55) 
        
44754563535486898023760406147845887138100226753724037248460285587734\
0726924157920380127788644000
CPU time: 0.00 s,  Wall time: 0.00 s
447545635354868980237604061478458871381002267537240372484602855877340726924157920380127788644000
CPU time: 0.00 s,  Wall time: 0.00 s
sys.setrecursionlimit(2000) 
       
time num_of_partitions(500, 250) 
        
12968140938681565914995612307114049718312816545966687321175690264267\
56739703856363800950644188543874136543268023589088351758963601321890\
43627514122540412529602530574964237040179788828178875194503428251067\
88617351227429703762892323539498143829263644537861261519232275295982\
91396386576594180741573746673369922420878438081108723641817748775600\
15257135664708406748283456533315722630025486607950679592277016618355\
56392295097157738983575389094164071704429392118761857783271628467228\
52407390253102769381762295879807451335169622139964709297551222075784\
50747566076439072259027699178623224885133113242035107040508034674081\
21449476704433359406493781499812626827727051958696986975496020201552\
91132000
CPU time: 0.78 s,  Wall time: 0.79 s
1296814093868156591499561230711404971831281654596668732117569026426756739703856363800950644188543874136543268023589088351758963601321890436275141225404125296025305749642370401797888281788751945034282510678861735122742970376289232353949814382926364453786126151923227529598291396386576594180741573746673369922420878438081108723641817748775600152571356647084067482834565333157226300254866079506795922770166183555639229509715773898357538909416407170442939211876185778327162846722852407390253102769381762295879807451335169622139964709297551222075784507475660764390722590276991786232248851331132420351070405080346740812144947670443335940649378149981262682772705195869698697549602020155291132000
CPU time: 0.78 s,  Wall time: 0.79 s
time stirling_number2(500, 250) 
        
12968140938681565914995612307114049718312816545966687321175690264267\
56739703856363800950644188543874136543268023589088351758963601321890\
43627514122540412529602530574964237040179788828178875194503428251067\
88617351227429703762892323539498143829263644537861261519232275295982\
91396386576594180741573746673369922420878438081108723641817748775600\
15257135664708406748283456533315722630025486607950679592277016618355\
56392295097157738983575389094164071704429392118761857783271628467228\
52407390253102769381762295879807451335169622139964709297551222075784\
50747566076439072259027699178623224885133113242035107040508034674081\
21449476704433359406493781499812626827727051958696986975496020201552\
91132000
CPU time: 0.00 s,  Wall time: 0.01 s
1296814093868156591499561230711404971831281654596668732117569026426756739703856363800950644188543874136543268023589088351758963601321890436275141225404125296025305749642370401797888281788751945034282510678861735122742970376289232353949814382926364453786126151923227529598291396386576594180741573746673369922420878438081108723641817748775600152571356647084067482834565333157226300254866079506795922770166183555639229509715773898357538909416407170442939211876185778327162846722852407390253102769381762295879807451335169622139964709297551222075784507475660764390722590276991786232248851331132420351070405080346740812144947670443335940649378149981262682772705195869698697549602020155291132000
CPU time: 0.00 s,  Wall time: 0.01 s
Memoization Decorator:
def remember(f, cache = {}):
   def g(*args):
       key = (f, tuple(args))
       if key not in cache:
           cache[key] = f(*args)
       return cache[key]
   return g 
       
@remember
def num_of_partitions(n, k):
   if n == 0 and k == 0:
       return 1
   if n == 0 or k == 0:
       return 0
   if n > 0 and k > 0:    
       return num_of_partitions(n-1, k-1) + k * num_of_partitions(n-1, k)

   raise ValueError, "The number of Partitions is not defined for negative parameters" 
       
time num_of_partitions(500, 250) 
        
12968140938681565914995612307114049718312816545966687321175690264267\
56739703856363800950644188543874136543268023589088351758963601321890\
43627514122540412529602530574964237040179788828178875194503428251067\
88617351227429703762892323539498143829263644537861261519232275295982\
91396386576594180741573746673369922420878438081108723641817748775600\
15257135664708406748283456533315722630025486607950679592277016618355\
56392295097157738983575389094164071704429392118761857783271628467228\
52407390253102769381762295879807451335169622139964709297551222075784\
50747566076439072259027699178623224885133113242035107040508034674081\
21449476704433359406493781499812626827727051958696986975496020201552\
91132000
CPU time: 1.34 s,  Wall time: 1.36 s
1296814093868156591499561230711404971831281654596668732117569026426756739703856363800950644188543874136543268023589088351758963601321890436275141225404125296025305749642370401797888281788751945034282510678861735122742970376289232353949814382926364453786126151923227529598291396386576594180741573746673369922420878438081108723641817748775600152571356647084067482834565333157226300254866079506795922770166183555639229509715773898357538909416407170442939211876185778327162846722852407390253102769381762295879807451335169622139964709297551222075784507475660764390722590276991786232248851331132420351070405080346740812144947670443335940649378149981262682772705195869698697549602020155291132000
CPU time: 1.34 s,  Wall time: 1.36 s

Beispiel 26

Die Chebyshev-Polynome sind definiert durch die Rekursionsformel: T_0(x) = 1 \quad T_1(x) = x und für n > 1:
T_{n+1}(x) = 2x T_n(x) - T_{n-1}(x).
Schreiben Sie eine Funktion chebyshev(n) die das n-te Chebyshev-Polynom berechnet.
  1. Berechnen Sie die ersten 10 Chebyshev-Polynome.
  2. Schreiben Sie eine Tabelle der ersten 10 Chebyshev-Polynome in die Datei tabelle.tex. Schreiben Sie ein LaTeX-Dokument chebyshev.tex welches die Datei tabelle.tex inkludiert und die Tabelle ausgibt. Das Ergebnis soll ungefähr folgendermassen aussehen:
    \begin{align*} T_0(x) &= 1\\ T_1(x) &= x\\ &\vdots \end{align*}
  3. Erzeugen Sie den Graphen der Chebyshev-Polynome T_0(x),\cdots, T_5(x) (alle Polynome sollen gemeinsam in ein Bild gezeichnet werden).
  4. Finden Sie heraus wie man Sage Grafiken in eine PDF-Datei exportieren kann. Exportieren Sie den Graphen aus Punkt 3, und binden Sie in das Dokument chebyshev.tex ein.
P.<x> = QQ[] 
       
Mit Memoization:
@remember
def chebyshev(n):
 if n == 0:
   return P(1)
 if n == 1:
   return x
 else:
   return 2 * x * chebyshev(n - 1) - chebyshev(n - 2) 
       
Iterativ:
def chebyshev(n):
 if n == 0:
   return P(1)

 cold, cnew = P(1), x

 for i in xrange(n - 1):
   cold, cnew = cnew, 2 * x * cnew - cold
 return cnew 
       
for i in [0..10]:
 view(chebyshev(i)) 
        
1
x
2 x^{2} - 1
4 x^{3} - 3 x
8 x^{4} - 8 x^{2} + 1
16 x^{5} - 20 x^{3} + 5 x
32 x^{6} - 48 x^{4} + 18 x^{2} - 1
64 x^{7} - 112 x^{5} + 56 x^{3} - 7 x
128 x^{8} - 256 x^{6} + 160 x^{4} - 32 x^{2} + 1
256 x^{9} - 576 x^{7} + 432 x^{5} - 120 x^{3} + 9 x
512 x^{10} - 1280 x^{8} + 1120 x^{6} - 400 x^{4} + 50 x^{2} - 1
1
x
2 x^{2} - 1
4 x^{3} - 3 x
8 x^{4} - 8 x^{2} + 1
16 x^{5} - 20 x^{3} + 5 x
32 x^{6} - 48 x^{4} + 18 x^{2} - 1
64 x^{7} - 112 x^{5} + 56 x^{3} - 7 x
128 x^{8} - 256 x^{6} + 160 x^{4} - 32 x^{2} + 1
256 x^{9} - 576 x^{7} + 432 x^{5} - 120 x^{3} + 9 x
512 x^{10} - 1280 x^{8} + 1120 x^{6} - 400 x^{4} + 50 x^{2} - 1
datei = open("tabelle.tex", 'w')
datei.write("\\begin{align*}\n")
for i in [0..10]:
 datei.write("T_{%d}(x) &= %s \\\\\n" % (i, latex(chebyshev(i))))
datei.write("\\end{align*}\n")
datei.close() 
       
g = Graphics()
for i in [0..5]:
 g = g + chebyshev(i).plot(-1, 1, hue = i/6)

g.show() 
       
g.save("chebyshev.pdf") 
       

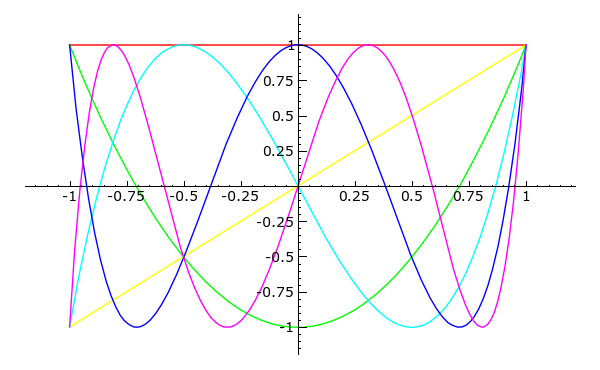Beispiel 27

Eine Hypotrochoide ist eine in Parameterform definierte Kurve:
\begin{align*} x(\phi) & = (R-r) \cos(\phi) + d \cos\left(\frac{R-r}{r} \phi\right) \\ y(\phi) & = (R-r) \sin(\phi) - d \sin\left(\frac{R-r}{r} \phi\right) \end{align*}
Zeichnen Sie die Hypotrochoide für die Parameter (R = 5, r = 4, d = 2) und 0 \leq \phi \leq 8\pi.
def hypotrochoid(R, r, d):
   xcoord = lambda phi: (R - r) * cos(RDF(phi)) + d * cos((R - r)/r * RDF(phi))
   ycoord = lambda phi: (R - r) * sin(RDF(phi)) - d * sin((R - r)/r * RDF(phi))
   return (xcoord, ycoord) 
       
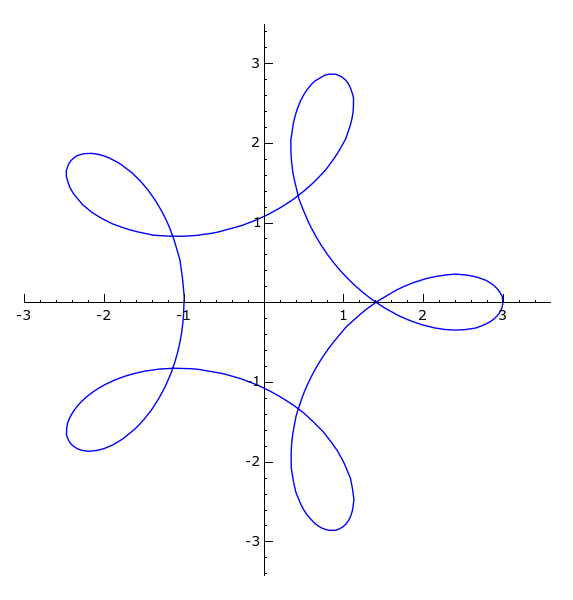parametric_plot(hypotrochoid(5, 4, 2), 0, 8*pi).show(aspect_ratio = 1)