Computermathematik (für Informatik)
4. Übungsblatt
3. 12. 2008
Die heutigen Übungen sollen mit dem Computeralgebrasystem Sage gelöst werden.
Die Lösung der Beispiele soll auf möglichst kompakte Weise erfolgen. Wenn zum Beispiel eine Funktion für mehrere Werte berechnet werden soll, soll das mittels einer geeigneten Schleifen oder Listen Operation erfolgen, und nicht alle Werte einzeln eingetippt werden.
Zwischenergebnisse welche in einem weiteren Berechnungsschritt benötigt werden, sollen in eine Variable gespeichert und weiterverwendet werden (nicht neu eintippen).
Beispiel 28
Wir betrachten die durch
- Bestimmen Sie die ersten 20 Folgenglieder mit 1000 Bits Genauigkeit.
- Bestimmen Sie das erste Folgenglied a_{n_\varepsilon} dass von 2 einen Abstand von weniger als \varepsilon hat. Für \varepsilon = 10^{-2},\, 10^{-3},\, 10^{-4}. Geben Sie auch jeweils den Index n_\epsilon an.
- Bestimmen Sie das erste Folgenglied a_{n_\varepsilon} das vom nächsten Folgenglied a_{n_\varepsilon + 1} einen Abstand von weniger als \varepsilon hat. Für \varepsilon = 10^{-6},\, 10^{-7},\, 10^{-8}. Geben Sie auch jeweils den Index n_\varepsilon an.
-
Wir bilden eine neue Folge b_n durch
b_n = a_{n+2} - \frac{(a_{n+2}-a_{n+1})^2}{a_{n+2}-2a_{n+1}+a_n},dann hat b_n genau den selben Grenzwert wie die Folge a_n. Berechnen Sie Punkt (b) für die Folge b_n. Was fällt auf?
Iterative Lösung
R = RealField(1000)
a = R(1)
print a
for n in xrange(n - 1):
a = 1/4 * a^2 + 1
print a
1.000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000 1.250000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000 1.390625000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000 1.483459472656250000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000 1.550163001753389835357666015625000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000 1.600751333001270024442366790573544221842894330620765686035156250000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000 1.640601207526335718909531014083287426094068189973652077967476847960\ 50739012560441278890804861489982613420579582452774047851562500000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000 1.672893080534217720184351975004490885766135050007179404367249744466\ 16783158246607608752050754999137235007298644591897995604494232989047\ 84348382129876408454371899717487831805679277284582546047838071462416\ 96539812554914150588558641175040975213050842285156250000000000000000\ 00000000000000000000000000000 1.699642814724816163726236514774414531751313379800628855835955854897\ 14009265208540458080618535478043137145973618523605532434230752095185\ 57895535075236312384314362640812544885798787838949256588186582159130\ 05487633567997557451244703372428445433596745662593155550369470324600\ 05496569726996407447095673968 1.722196424411423941205512295600073869390644155105732214945076460616\ 50912125800945189448907987462331301277297181343412144988560329921401\ 02405901350375571172253469319616227880289844647205897891118220615448\ 38327107929589126364992405032511841110174614461114331619058723936797\ 88470808229754141795917912824 1.741490131063873364188377177134508285550633713018408760025135756325\ 26811262436597818612474403551811535262346257799399082178347336132402\ 18550232594461264640708781996636983828131486579498593521090746204051\ 49379847088244899996829720274290957078077796952160951068662841713419\ 00548017715677768536168922242 1.758196969148216706934933791105877785423153208567009800057101050932\ 93539483800080760651889147548803666030701700967052928793679987529631\ 17494638091765910875889757355060667970760125317280902167714974432965\ 73362606645463758704081009707285749790338436847305521844248313593629\ 39756204346029639879827960250 1.772814145580493822699572983922675752849138126597470304187391244346\ 80377504259700988473064961624861835309657998163377973335570078842547\ 51068448267325779678293515948974206022589742124239480431655900516579\ 54347874370080366550858875207473343933082778607158082850974256917102\ 11221234780913743289851600433 1.785717498692574086317705805227079399174697951023078915341726450843\ 54610920006327527356839378170682357075185675913099405574654577153698\ 80681926848009982404087486437565531199722752518071815276408405631589\ 34694337810774308424029160647173159433992762967730108007836179406985\ 85268661025909162206006729865 1.797196746284215833419359538064789026132045958338499032277979746212\ 91674427032329168376786958512709689867675734362290440281814461899598\ 40930461255577283304155838703196925445721981569298898522873079696474\ 81966603741240034172099201038330208836069330905867358507038190422066\ 07303751495722268993104010287 1.807479036213643014511670167598616269983266197381368427722948747406\ 75468296240928205985979166699269434342806772010919682084378134102522\ 65688477603641462105455072602295316836334512124152017981116515673983\ 14373252014058603564289378145105475425760640199626477819238600809241\ 65258532302012198857871955220 1.816745116587949958970254637052961112756913212464061140792405578573\ 62972560403603444704092841212920580384728808996217642547082821275810\ 70039745691080562653456217843162829162619264341028996210065594144901\ 92082543409288571475812381579098530082376099648192122327840457455153\ 20444266442065784464975004634 1.825140704661540972292226539134440895257169067181200220136179183467\ 58487621813651159776640348116116612626374511904458172259675397469485\ 41501764100571204983795208805811386154136022656305628209453063415522\ 23545108849685539577316182378666434439064986932641868021372571301742\ 33578901317652975994115747657 1.832784647953106582056548534186994613500976027967171669022893376569\ 33507492274618032340244241449176528794057781428912077038986740338396\ 92175927152495212492197421889469269022575503629674476757841697251872\ 50443276102352661078220876502930726199734935027463260630228314075790\ 20670346763471561547189357763 1.839774891443148207751046958824018248416981618429475009977556082226\ 89415165825325789132304265822101425013553071842552863896409337334496\ 43587561238321446458594409038084642127831598396293759009373541772473\ 52929423074016513636681731246812552477899487189768057200824220638102\ 89453769968984168008038767840 1.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 1.25000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 1.39062500000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 1.48345947265625000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 1.55016300175338983535766601562500000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 1.60075133300127002444236679057354422184289433062076568603515625000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 1.64060120752633571890953101408328742609406818997365207796747684796050739012560441278890804861489982613420579582452774047851562500000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 1.67289308053421772018435197500449088576613505000717940436724974446616783158246607608752050754999137235007298644591897995604494232989047843483821298764084543718997174878318056792772845825460478380714624169653981255491415058855864117504097521305084228515625000000000000000000000000000000000000000000000 1.69964281472481616372623651477441453175131337980062885583595585489714009265208540458080618535478043137145973618523605532434230752095185578955350752363123843143626408125448857987878389492565881865821591300548763356799755745124470337242844543359674566259315555036947032460005496569726996407447095673968 1.72219642441142394120551229560007386939064415510573221494507646061650912125800945189448907987462331301277297181343412144988560329921401024059013503755711722534693196162278802898446472058978911182206154483832710792958912636499240503251184111017461446111433161905872393679788470808229754141795917912824 1.74149013106387336418837717713450828555063371301840876002513575632526811262436597818612474403551811535262346257799399082178347336132402185502325944612646407087819966369838281314865794985935210907462040514937984708824489999682972027429095707807779695216095106866284171341900548017715677768536168922242 1.75819696914821670693493379110587778542315320856700980005710105093293539483800080760651889147548803666030701700967052928793679987529631174946380917659108758897573550606679707601253172809021677149744329657336260664546375870408100970728574979033843684730552184424831359362939756204346029639879827960250 1.77281414558049382269957298392267575284913812659747030418739124434680377504259700988473064961624861835309657998163377973335570078842547510684482673257796782935159489742060225897421242394804316559005165795434787437008036655085887520747334393308277860715808285097425691710211221234780913743289851600433 1.78571749869257408631770580522707939917469795102307891534172645084354610920006327527356839378170682357075185675913099405574654577153698806819268480099824040874864375655311997227525180718152764084056315893469433781077430842402916064717315943399276296773010800783617940698585268661025909162206006729865 1.79719674628421583341935953806478902613204595833849903227797974621291674427032329168376786958512709689867675734362290440281814461899598409304612555772833041558387031969254457219815692988985228730796964748196660374124003417209920103833020883606933090586735850703819042206607303751495722268993104010287 1.80747903621364301451167016759861626998326619738136842772294874740675468296240928205985979166699269434342806772010919682084378134102522656884776036414621054550726022953168363345121241520179811165156739831437325201405860356428937814510547542576064019962647781923860080924165258532302012198857871955220 1.81674511658794995897025463705296111275691321246406114079240557857362972560403603444704092841212920580384728808996217642547082821275810700397456910805626534562178431628291626192643410289962100655941449019208254340928857147581238157909853008237609964819212232784045745515320444266442065784464975004634 1.82514070466154097229222653913444089525716906718120022013617918346758487621813651159776640348116116612626374511904458172259675397469485415017641005712049837952088058113861541360226563056282094530634155222354510884968553957731618237866643443906498693264186802137257130174233578901317652975994115747657 1.83278464795310658205654853418699461350097602796717166902289337656933507492274618032340244241449176528794057781428912077038986740338396921759271524952124921974218894692690225755036296744767578416972518725044327610235266107822087650293072619973493502746326063022831407579020670346763471561547189357763 1.83977489144314820775104695882401824841698161842947500997755608222689415165825325789132304265822101425013553071842552863896409337334496435875612383214464585944090380846421278315983962937590093735417724735292942307401651363668173124681255247789948718976805720082422063810289453769968984168008038767840 |
a = 1.0
n = 0
while abs(a - 2) > epsilon:
n += 1
a = 1/4.0 * a^2.0 + 1.0
return a, n
epsilon = 10^i
a_n, n = bsp28b(epsilon)
html("$\\varepsilon = 10^{%d},\quad n_\\varepsilon = %i,\quad a_{n_\\varepsilon} = %f$" % (i, n, a_n))
\varepsilon = 10^{-2},\quad n_\varepsilon = 392,\quad a_{n_\varepsilon} = 1.990019 \varepsilon = 10^{-3},\quad n_\varepsilon = 3989,\quad a_{n_\varepsilon} = 1.999000 \varepsilon = 10^{-4},\quad n_\varepsilon = 39987,\quad a_{n_\varepsilon} = 1.999900 \varepsilon = 10^{-2},\quad n_\varepsilon = 392,\quad a_{n_\varepsilon} = 1.990019 \varepsilon = 10^{-3},\quad n_\varepsilon = 3989,\quad a_{n_\varepsilon} = 1.999000 \varepsilon = 10^{-4},\quad n_\varepsilon = 39987,\quad a_{n_\varepsilon} = 1.999900 |
a_0 = 1.0
a_1 = 1/4 * a_0 ^ 2 + 1
n = 0
while abs(a_0 - a_1) > epsilon:
n += 1
a_0, a_1 = a_1, 1/4 * a_1^2 + 1
return a_0, n
epsilon = 10^i
a_n, n = bsp28c(epsilon)
html("$\\varepsilon = 10^{%d},\quad n_\\varepsilon = %i,\quad a_{n_\\varepsilon} = %f$" % (i, n, a_n))
\varepsilon = 10^{-6},\quad n_\varepsilon = 1990,\quad a_{n_\varepsilon} = 1.998000 \varepsilon = 10^{-7},\quad n_\varepsilon = 6314,\quad a_{n_\varepsilon} = 1.999368 \varepsilon = 10^{-8},\quad n_\varepsilon = 19988,\quad a_{n_\varepsilon} = 1.999800 \varepsilon = 10^{-6},\quad n_\varepsilon = 1990,\quad a_{n_\varepsilon} = 1.998000 \varepsilon = 10^{-7},\quad n_\varepsilon = 6314,\quad a_{n_\varepsilon} = 1.999368 \varepsilon = 10^{-8},\quad n_\varepsilon = 19988,\quad a_{n_\varepsilon} = 1.999800 |
a_0 = 1.0
a_1 = 1/4 * a_0 ^ 2 + 1
a_2 = 1/4 * a_1 ^ 2 + 1
b = a_2 - (a_2 - a_1)^2 / (a_2 - 2 * a_1 + a_0)
n = 0
while abs(b - 2) > epsilon:
n += 1
a_0, a_1, a_2 = a_1, a_2, 1/4.0 * a_2 ^ 2.0 + 1.0
b = a_2 - (a_2 - a_1)^2 / (a_2 - 2 * a_1 + a_0)
return b, n
epsilon = 10^i
b_n, n = bsp28d(epsilon)
html("$\\varepsilon = 10^{%d},\quad n_\\varepsilon = %i,\quad b_{n_\\varepsilon} = %f$" % (i, n, b_n))
\varepsilon = 10^{-2},\quad n_\varepsilon = 192,\quad b_{n_\varepsilon} = 1.990028 \varepsilon = 10^{-3},\quad n_\varepsilon = 1990,\quad b_{n_\varepsilon} = 1.999000 \varepsilon = 10^{-4},\quad n_\varepsilon = 19982,\quad b_{n_\varepsilon} = 1.999900 \varepsilon = 10^{-2},\quad n_\varepsilon = 192,\quad b_{n_\varepsilon} = 1.990028 \varepsilon = 10^{-3},\quad n_\varepsilon = 1990,\quad b_{n_\varepsilon} = 1.999000 \varepsilon = 10^{-4},\quad n_\varepsilon = 19982,\quad b_{n_\varepsilon} = 1.999900 |
Lösung mit Generatoren
Ein Generator ist ein Python Konstrukt, dass eine Folge von Werten erzeugt.
Man erzeugt einen Generator, wie eine normale Python Funktion, allerdings wird das Schlüsselwort yield anstatt return verwendet um Werte zurückzugeben.
Wir definieren uns einen Generator für die natürlichen Zahlen:
n = 0
while True:
yield n
n += 1
type(nat)
<type 'generator'> <type 'generator'> |
0 1 2 0 1 2 |
Mit der Funktion iter kann man Listen in Generatoren umwandeln.
1 2 3 1 2 3 |
Eine Generator Comprehension ist das äquivalent einer List Comprehension nur eben für Generatoren.
Hier erzeugen wir uns aus dem Generator für die natürlichen Zahlen einen neuen Generator für die ungeraden Quadratzahlen.
1 9 25 1 9 25 |
l = []
for i in xrange(n):
try:
l.append(g.next())
except StopIteration:
break
return l
[49, 81, 121, 169, 225] [49, 81, 121, 169, 225] |
[1, 2, 3] [4, 5, 6] [7, 8, 9] [10] [1, 2, 3] [4, 5, 6] [7, 8, 9] [10] |
a = ring(1)
while True:
yield a
a = 1/4 * a^2 + 1
1.00000000000000 1.25000000000000 1.39062500000000 1.48345947265625 1.00000000000000 1.25000000000000 1.39062500000000 1.48345947265625 |
for a in alist:
print a
1.000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000 1.250000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000 1.390625000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000 1.483459472656250000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000 1.550163001753389835357666015625000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000 1.600751333001270024442366790573544221842894330620765686035156250000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000 1.640601207526335718909531014083287426094068189973652077967476847960\ 50739012560441278890804861489982613420579582452774047851562500000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000000000000000000000000000000000000000000\ 00000000000000000000000000000 1.672893080534217720184351975004490885766135050007179404367249744466\ 16783158246607608752050754999137235007298644591897995604494232989047\ 84348382129876408454371899717487831805679277284582546047838071462416\ 96539812554914150588558641175040975213050842285156250000000000000000\ 00000000000000000000000000000 1.699642814724816163726236514774414531751313379800628855835955854897\ 14009265208540458080618535478043137145973618523605532434230752095185\ 57895535075236312384314362640812544885798787838949256588186582159130\ 05487633567997557451244703372428445433596745662593155550369470324600\ 05496569726996407447095673968 1.722196424411423941205512295600073869390644155105732214945076460616\ 50912125800945189448907987462331301277297181343412144988560329921401\ 02405901350375571172253469319616227880289844647205897891118220615448\ 38327107929589126364992405032511841110174614461114331619058723936797\ 88470808229754141795917912824 1.741490131063873364188377177134508285550633713018408760025135756325\ 26811262436597818612474403551811535262346257799399082178347336132402\ 18550232594461264640708781996636983828131486579498593521090746204051\ 49379847088244899996829720274290957078077796952160951068662841713419\ 00548017715677768536168922242 1.758196969148216706934933791105877785423153208567009800057101050932\ 93539483800080760651889147548803666030701700967052928793679987529631\ 17494638091765910875889757355060667970760125317280902167714974432965\ 73362606645463758704081009707285749790338436847305521844248313593629\ 39756204346029639879827960250 1.772814145580493822699572983922675752849138126597470304187391244346\ 80377504259700988473064961624861835309657998163377973335570078842547\ 51068448267325779678293515948974206022589742124239480431655900516579\ 54347874370080366550858875207473343933082778607158082850974256917102\ 11221234780913743289851600433 1.785717498692574086317705805227079399174697951023078915341726450843\ 54610920006327527356839378170682357075185675913099405574654577153698\ 80681926848009982404087486437565531199722752518071815276408405631589\ 34694337810774308424029160647173159433992762967730108007836179406985\ 85268661025909162206006729865 1.797196746284215833419359538064789026132045958338499032277979746212\ 91674427032329168376786958512709689867675734362290440281814461899598\ 40930461255577283304155838703196925445721981569298898522873079696474\ 81966603741240034172099201038330208836069330905867358507038190422066\ 07303751495722268993104010287 1.807479036213643014511670167598616269983266197381368427722948747406\ 75468296240928205985979166699269434342806772010919682084378134102522\ 65688477603641462105455072602295316836334512124152017981116515673983\ 14373252014058603564289378145105475425760640199626477819238600809241\ 65258532302012198857871955220 1.816745116587949958970254637052961112756913212464061140792405578573\ 62972560403603444704092841212920580384728808996217642547082821275810\ 70039745691080562653456217843162829162619264341028996210065594144901\ 92082543409288571475812381579098530082376099648192122327840457455153\ 20444266442065784464975004634 1.825140704661540972292226539134440895257169067181200220136179183467\ 58487621813651159776640348116116612626374511904458172259675397469485\ 41501764100571204983795208805811386154136022656305628209453063415522\ 23545108849685539577316182378666434439064986932641868021372571301742\ 33578901317652975994115747657 1.832784647953106582056548534186994613500976027967171669022893376569\ 33507492274618032340244241449176528794057781428912077038986740338396\ 92175927152495212492197421889469269022575503629674476757841697251872\ 50443276102352661078220876502930726199734935027463260630228314075790\ 20670346763471561547189357763 1.839774891443148207751046958824018248416981618429475009977556082226\ 89415165825325789132304265822101425013553071842552863896409337334496\ 43587561238321446458594409038084642127831598396293759009373541772473\ 52929423074016513636681731246812552477899487189768057200824220638102\ 89453769968984168008038767840 1.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 1.25000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 1.39062500000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 1.48345947265625000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 1.55016300175338983535766601562500000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 1.60075133300127002444236679057354422184289433062076568603515625000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 1.64060120752633571890953101408328742609406818997365207796747684796050739012560441278890804861489982613420579582452774047851562500000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 1.67289308053421772018435197500449088576613505000717940436724974446616783158246607608752050754999137235007298644591897995604494232989047843483821298764084543718997174878318056792772845825460478380714624169653981255491415058855864117504097521305084228515625000000000000000000000000000000000000000000000 1.69964281472481616372623651477441453175131337980062885583595585489714009265208540458080618535478043137145973618523605532434230752095185578955350752363123843143626408125448857987878389492565881865821591300548763356799755745124470337242844543359674566259315555036947032460005496569726996407447095673968 1.72219642441142394120551229560007386939064415510573221494507646061650912125800945189448907987462331301277297181343412144988560329921401024059013503755711722534693196162278802898446472058978911182206154483832710792958912636499240503251184111017461446111433161905872393679788470808229754141795917912824 1.74149013106387336418837717713450828555063371301840876002513575632526811262436597818612474403551811535262346257799399082178347336132402185502325944612646407087819966369838281314865794985935210907462040514937984708824489999682972027429095707807779695216095106866284171341900548017715677768536168922242 1.75819696914821670693493379110587778542315320856700980005710105093293539483800080760651889147548803666030701700967052928793679987529631174946380917659108758897573550606679707601253172809021677149744329657336260664546375870408100970728574979033843684730552184424831359362939756204346029639879827960250 1.77281414558049382269957298392267575284913812659747030418739124434680377504259700988473064961624861835309657998163377973335570078842547510684482673257796782935159489742060225897421242394804316559005165795434787437008036655085887520747334393308277860715808285097425691710211221234780913743289851600433 1.78571749869257408631770580522707939917469795102307891534172645084354610920006327527356839378170682357075185675913099405574654577153698806819268480099824040874864375655311997227525180718152764084056315893469433781077430842402916064717315943399276296773010800783617940698585268661025909162206006729865 1.79719674628421583341935953806478902613204595833849903227797974621291674427032329168376786958512709689867675734362290440281814461899598409304612555772833041558387031969254457219815692988985228730796964748196660374124003417209920103833020883606933090586735850703819042206607303751495722268993104010287 1.80747903621364301451167016759861626998326619738136842772294874740675468296240928205985979166699269434342806772010919682084378134102522656884776036414621054550726022953168363345121241520179811165156739831437325201405860356428937814510547542576064019962647781923860080924165258532302012198857871955220 1.81674511658794995897025463705296111275691321246406114079240557857362972560403603444704092841212920580384728808996217642547082821275810700397456910805626534562178431628291626192643410289962100655941449019208254340928857147581238157909853008237609964819212232784045745515320444266442065784464975004634 1.82514070466154097229222653913444089525716906718120022013617918346758487621813651159776640348116116612626374511904458172259675397469485415017641005712049837952088058113861541360226563056282094530634155222354510884968553957731618237866643443906498693264186802137257130174233578901317652975994115747657 1.83278464795310658205654853418699461350097602796717166902289337656933507492274618032340244241449176528794057781428912077038986740338396921759271524952124921974218894692690225755036296744767578416972518725044327610235266107822087650293072619973493502746326063022831407579020670346763471561547189357763 1.83977489144314820775104695882401824841698161842947500997755608222689415165825325789132304265822101425013553071842552863896409337334496435875612383214464585944090380846421278315983962937590093735417724735292942307401651363668173124681255247789948718976805720082422063810289453769968984168008038767840 |
(0, 1.0) (1, 1.25) (2, 1.390625) (0, 1.0) (1, 1.25) (2, 1.390625) |
h = enumerate(g)
n, a = h.next()
while abs(limit - a) >= epsilon:
n, a = h.next()
return n, a
a_0 = g.next()
a_1 = g.next()
a_2 = g.next()
while True:
b = a_2 - (a_2 - a_1)^2 / (a_2 - 2*a_1 + a_0)
yield b
a_0, a_1, a_2 = a_1, a_2, g.next()
for e in epsilon:
print seq_lim(sequence(), e, 2), seq_lim(seq_accel(sequence()), e, 2)
(392, 1.99001896664) (192, 1.99002825175) (3989, 1.99900001548) (1990, 1.99900043432) (39987, 1.99990000091) (19982, 1.99990000001) (392, 1.99001896664) (192, 1.99002825175) (3989, 1.99900001548) (1990, 1.99900043432) (39987, 1.99990000091) (19982, 1.99990000001) |
h = enumerate(g)
n0, a0 = h.next()
n1, a1 = h.next()
while abs(a0 - a1) >= epsilon:
n0, a0 = n1, a1
n1, a1 = h.next()
return n0, a0
for e in epsilon:
print seq_diff(sequence(), e), seq_diff(seq_accel(sequence()), e)
(192, 1.98000641036) (134, 1.98593746254) (1990, 1.99800036876) (1404, 1.99858609494) (19988, 1.99980000671) (9619, 1.99979235363) (192, 1.98000641036) (134, 1.98593746254) (1990, 1.99800036876) (1404, 1.99858609494) (19988, 1.99980000671) (9619, 1.99979235363) |
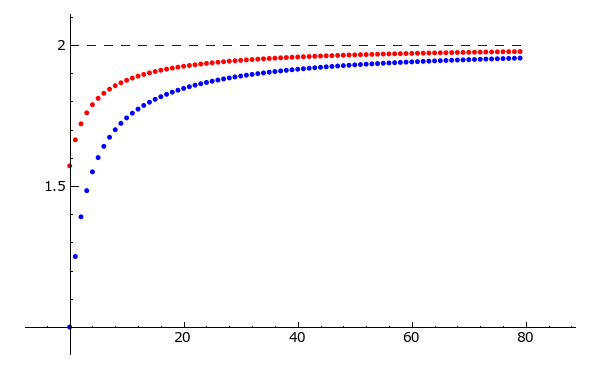
s1 = take(sequence(), n)
s2 = take(seq_accel(sequence()), n)
list_plot(s1) + \
list_plot(s2, rgbcolor = 'red') + \
line([(0, 2),(80, 2)], linestyle = '--')
 |
Beispiel 29a
Trapezregel
- Schreiben Sie eine Funktion trapez(f, a, b, n) die das Integral \int_a^b f(x) dxnäherungsweise mit Hilfe der Trapezregel mit Schrittweite h = \frac{b-a}{n} berechnet.
Die Trapezregel besagt:\int_a^b f(x) dx \approx h \cdot \sum_{i=1}^n f\left(a \ + \ h \cdot \frac{2i - 1}{2}\right). - Die Fehlerabschätzung für diese Approximation lautet: \left| E(f) \right| \le \frac{b - a}{24} \ h^2 \max_{a \le x \le b} {\left| f''(x) \right|}
Erweitern Sie ihre Funktion trapez, so dass sie sowohl eine Näherung für das Integral, als auch die Fehlerabschätzung berechnet.
Überprüfen Sie ihre Funktion anhand einiger Beispiele, und vergleichen Sie das Ergebnis mit der eingebauten Funktion integral_numerical.
h = RDF((b - a) / n)
a = RDF(a)
b = RDF(b)
integral_approx = h * sum([f(a + h * (2*i - 1)/2) for i in [1..n]])
return integral_approx
trapez(x^2, 0, 1, 100)
0.333325 0.333325 |
(0.33333333333333331, 3.7007434154171879e-15) (0.33333333333333331, 3.7007434154171879e-15) |
0.7500125 0.7500125 |
(0.75000000000000011, 8.3266726846886756e-15) (0.75000000000000011, 8.3266726846886756e-15) |
0.0542101327528 0.0542101327528 |
(0.054286809695038393, 6.0270466056875793e-16) (0.054286809695038393, 6.0270466056875793e-16) |
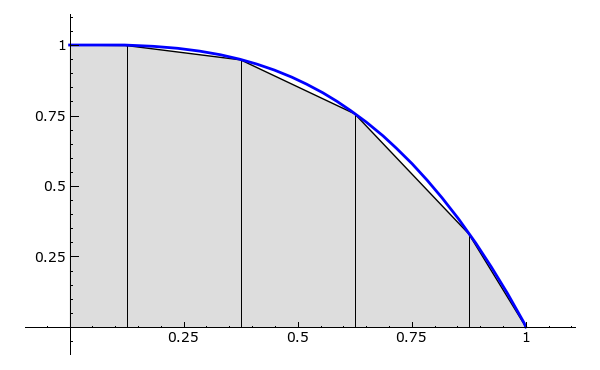
h = RDF((b - a) / n)
points = [(a, 0), (a, RDF(f(a)))] + \
[(a + h * (2*i - 1)/2, RDF(f(a + h * (2*i - 1)/2))) for i in [1..n]] + \
[(b, RDF(f(b))), (b, 0)]
p = polygon(points, rgbcolor = '#ddd')
for point in points:
p += line2d([(point[0], 0), point], rgbcolor = 'black')
for i in xrange(len(points) - 1):
p += line2d([points[i], points[i + 1]], rgbcolor = 'black')
p += plot(f, a, b, thickness = 2)
return p
 |
 |
h = RDF((b - a) / n)
a = RDF(a)
b = RDF(b)
integral_approx = h * sum([f(a + h * (2*i - 1)/2) for i in [1..n]])
f2(x) = f.diff().diff()
maximum, estimate = find_maximum_on_interval(lambda x: abs(f2(x)), a, b)
error_approx = RDF((b - a) / 24 * h^2 * maximum)
return (integral_approx, error_approx)
time trapez(x^2, 0, 1, 10)
(0.3325, 0.000833333333333) Time: CPU 2.02 s, Wall: 4.14 s (0.3325, 0.000833333333333) Time: CPU 2.02 s, Wall: 4.14 s |
(0.75125, 0.00249999992825) CPU time: 1.92 s, Wall time: 4.36 s (0.75125, 0.00249999992825) CPU time: 1.92 s, Wall time: 4.36 s |
(0.75000000000000011, 8.3266726846886756e-15) (0.75000000000000011, 8.3266726846886756e-15) |
(0.0524144255673, 0.035345983166) CPU time: 1.73 s, Wall time: 4.72 s (0.0524144255673, 0.035345983166) CPU time: 1.73 s, Wall time: 4.72 s |
(0.054286809695038393, 6.0270466056875793e-16) (0.054286809695038393, 6.0270466056875793e-16) |
Die obige Implementierung von trapez ist sehr langsam. Man kann die Performance dramatisch verbessern, wenn man die Funktionen f und f'' in eine Form konvertiert, die für numerische Berechnungen optimiert ist, das geht mit der Funktion fast_float, aus dem Paket sage.ext.fast_eval.
h = RDF((b - a) / n)
a = RDF(a)
b = RDF(b)
from sage.ext.fast_eval import fast_float, is_fast_float
# Konvertiere Symbolische Ausdruecke in eine Form
# die effizienter fÃÆür Fliesskommazahlen ist.
if not is_fast_float(f):
ff = fast_float(f)
else:
ff = f
integral_approx = h * sum([ff(a + h * (2*i - 1)/2) for i in [1..n]])
try:
f2 = f.diff().diff()
if not is_fast_float(f2):
f2 = fast_float(f2)
maximum, estimate = find_maximum_on_interval(lambda x: abs(f2(x)), a, b)
error_approx = RDF((b - a) / 24 * h^2 * maximum)
return (integral_approx, error_approx)
except AttributeError:
# Wenn f kein symbolischer Ausdruck ist, koennen wir
# keine Fehlerschranke berechnen.
return (integral_approx, "no error estimate available")
(0.7500005, 9.999999713e-07) CPU time: 0.06 s, Wall time: 0.15 s (0.7500005, 9.999999713e-07) CPU time: 0.06 s, Wall time: 0.15 s |
(0.333333, 3.33333333333e-07) CPU time: 0.07 s, Wall time: 0.26 s (0.333333, 3.33333333333e-07) CPU time: 0.07 s, Wall time: 0.26 s |
(2.00000328987, 5.16771278005e-06) CPU time: 0.06 s, Wall time: 0.16 s (2.00000328987, 5.16771278005e-06) CPU time: 0.06 s, Wall time: 0.16 s |
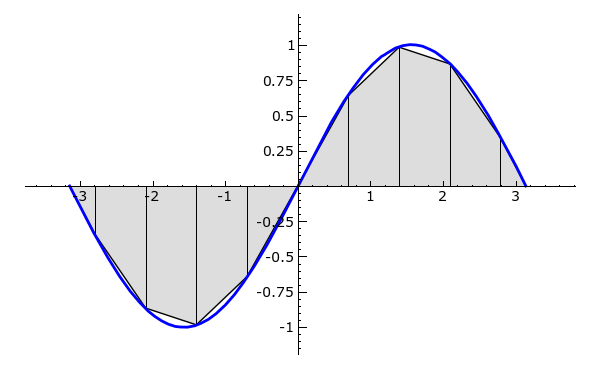
return sin(x)
time trapez_fast(f, 0, pi, 500)
(2.00000328987, 'no error estimate available') Time: CPU 0.16 s, Wall: 0.16 s (2.00000328987, 'no error estimate available') Time: CPU 0.16 s, Wall: 0.16 s |
Beispiel 30
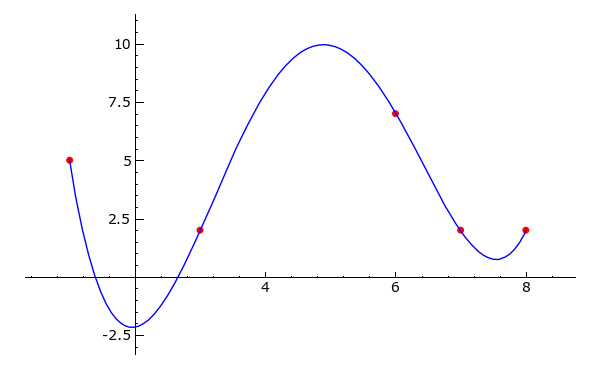
Das Interpolations Polynom p(x) zu den Stützen-
Berechnen Sie das Interpolations Polynom für die Stützwerte:
(1,\, 5),\, (3,\, 2),\, (6,\, 7),\, (7,\, 2),\, (8,\, 2)
-
Schreiben Sie eine Funktion in Sage, die für n im Interval [-1, 1] gleichmässig verteilte Werte x_i die Funktion
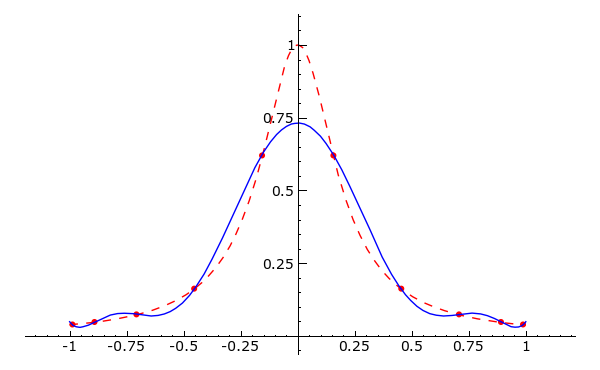
f(x) = \frac{1}{1+ 25 x^2}berechnet, und aus diesen Daten das zugehörige Interpolationspolynom bestimmt.Verleichen Sie die Interpolationspolynome für n=6, 10, 20 graphisch mit der Funktion f(x). Wird die Funktion gut approximiert?
-
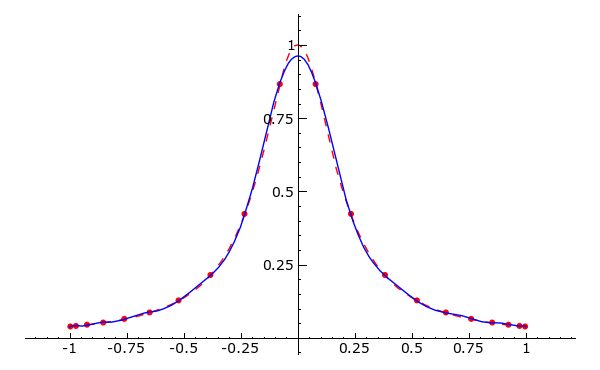
Machen Sie das selbe wie in Punkt (b) nur wählen Sie diesmal n Stützstellen
der Form
x_i = \cos\left(\frac{2i-1}{2n} \pi\right).Wird die Funktion gut approximiert?
"/local/data/huss/software/sage-3.3.alpha0/local/share/maxima/5.16.3\ /share/numeric/interpol.mac" "/local/data/huss/software/sage-3.3.alpha0/local/share/maxima/5.16.3/share/numeric/interpol.mac" |
f = maxima.lagrange(points).sage()
view(f)
\frac{{73 {x}^{4} }}{420} - \frac{{701 {x}^{3} }}{210} + \frac{{8957 {x}^{2} }}{420} - \frac{{5288 x}}{105} + \frac{186}{5}\frac{{73 {x}^{4} }}{420} - \frac{{701 {x}^{3} }}{210} + \frac{{8957 {x}^{2} }}{420} - \frac{{5288 x}}{105} + \frac{186}{5} |
True True |
p2 = plot(f, (x, 1, 8))
(p1 + p2).show()
 |
return RDF(1/(1+25*x^2))
def bsp30b(n):
data = [(x, f(x)) for x in xsrange(-1, 1, 2/(n - 1), include_endpoint = True)]
polynom = maxima.lagrange(data).sage()
g = plot(f, -1, 1, rgbcolor = 'red', linestyle='--')
g += plot(polynom, -1, 1)
g += list_plot(data, rgbcolor = 'red', pointsize = 15)
return g
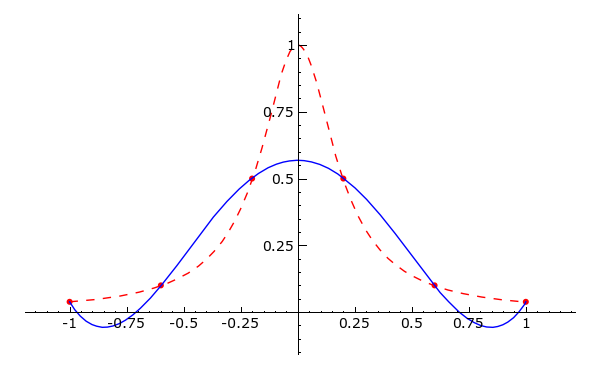 |
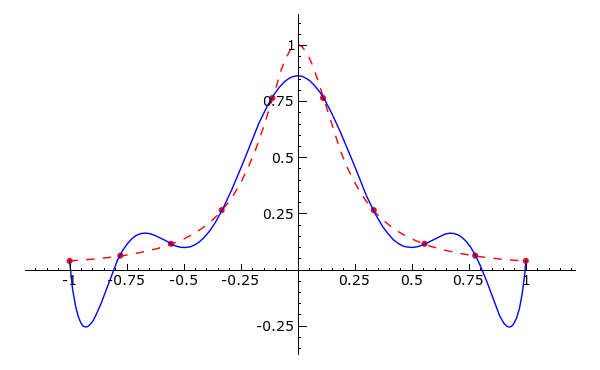 |
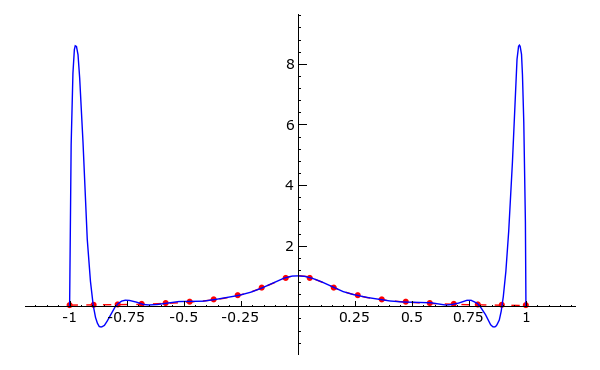 |
def bsp30c(n):
data = [(x, f(x)) for x in [RDF(cos((2*i-1)/(2*n)*pi)) for i in xrange(1, n + 1)]]
polynom = maxima.lagrange(data).sage()
g = plot(f, -1, 1, rgbcolor = 'red', linestyle='--')
g += plot(polynom, -1, 1)
g += list_plot(data, rgbcolor = 'red', pointsize = 15)
return g
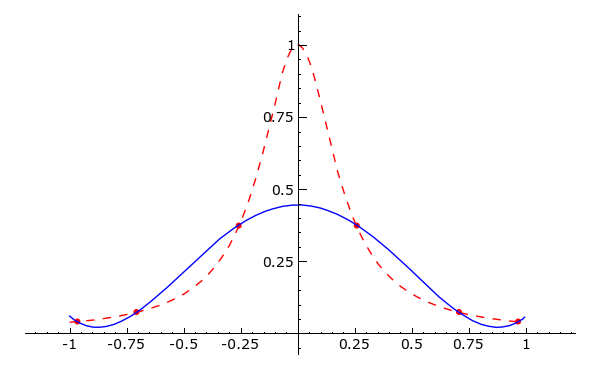 |
 |
 |
def f(x):
return RDF(1/(1+25*x^2))
def interpolate_data(n, points = 'uniform'):
if points == 'uniform':
return [(x, f(x)) for x in xsrange(-1, 1, 2/(n - 1), include_endpoint = True)]
else:
return [(x, f(x)) for x in [RDF(cos((2*i-1)/(2*n)*pi)) for i in xrange(1, n + 1)]]
def interpolate_polynom(data):
return maxima.lagrange(data).sage()
def interpolate_plot(n, points = 'uniform', color = 'red'):
data = interpolate_data(n, points = points)
p1 = plot(f, -1, 1, thickness = 2, linestyle = '--')
p2 = list_plot(data, pointsize = 20, rgbcolor = color)
p3 = plot(interpolate_polynom(data), -1, 1, rgbcolor = color)
return p1 + p2 + p3
@interact
def bsp30_interact(n = slider(3, vmax=30,step_size=1,default=3,label="interpolation order"), all = False, points = ['uniform', 'chebyshev']):
if all:
p = Graphics()
for i in xrange(3, n + 1, 2):
p += interpolate_plot(i, points = points, color = hue(i/n))
p
else:
p = interpolate_plot(n, points = points)
p.show(ymin = 0, ymax = 1)
Click to the left again to hide and once more to show the dynamic interactive window |