Computermathematik (für Informatik)

5. Übungsblatt
14. 1. 2009

Die heutigen Übungen sollen mit dem Computeralgebrasystem Sage gelöst werden.

Die Lösung der Beispiele soll auf möglichst kompakte Weise erfolgen. Wenn zum Beispiel eine Funktion für mehrere Werte berechnet werden soll, soll das mittels einer geeigneten Schleifen oder Listen Operation erfolgen, und nicht alle Werte einzeln eingetippt werden.

Zwischenergebnisse welche in einem weiteren Berechnungsschritt benötigt werden, sollen in eine Variable gespeichert und weiterverwendet werden (nicht neu eintippen).

Beispiel 31

Die Datei bsp31.data enthält numerische Daten von der Form:

\begin{align*} x_1\quad& f(x_1) \\ x_2\quad& f(x_2) \\ \vdots& \\ x_n\quad& f(x_n) \end{align*}

Wir wissen die Funktion f ist ungefähr von der Form

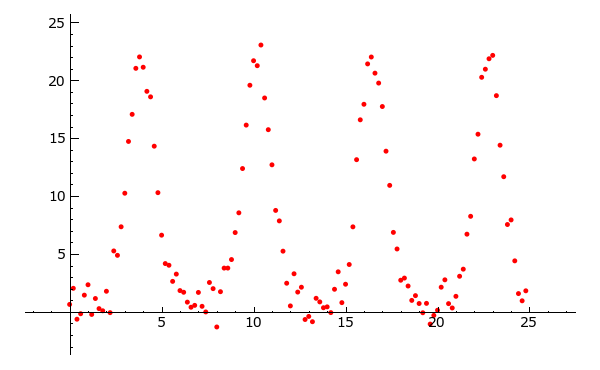
f(x) = a \cdot\exp(-b\cdot\sin(c\cdot x + \varphi)).

Lesen Sie die Datei bsp31.data in Sage ein, und geben Sie die Daten grafisch aus.
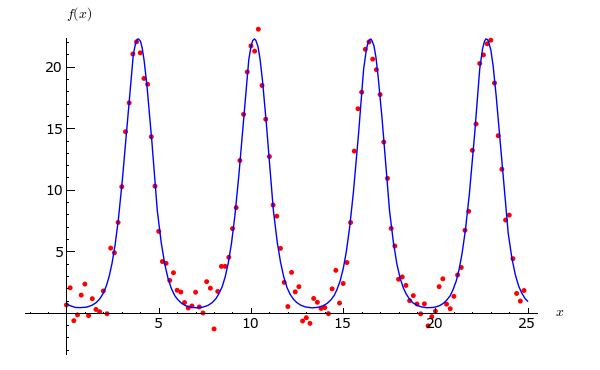
Hinweis: Sie können die Funktion get_remote_file verwenden um eine Datei direkt aus dem Internet in Sage zu laden.
Bestimmen Sie die reellen Parameter a, b und c derart, dass f die Daten möglichst gut interpoliert. Visualisieren Sie ihr Ergebnis.

Hinweis: Verwenden Sie die Funktion find_fit. Sie finden diese Funktion in Datei find_fit.sage auf der Homepage der Vorlesung.

Wir können die Datei find_fit.sage an das Notebook anhängen, und mittels load einlesen.

load find_fit.sage

find_fit?

Wir können die Daten direkt aus dem Internet laden:

url = 'http://www.math.tugraz.at/~huss/computermathematik08/dateien/bsp31.data'
datei = open(get_remote_file(url))
data = [map(float, line.split()) for line in datei.readlines()]
datei.close()

Attempting to load remote file:
http://www.math.tugraz.at/~huss/computermathematik08/dateien/bsp31.d\
ata
Loading: [.]

Attempting to load remote file: http://www.math.tugraz.at/~huss/computermathematik08/dateien/bsp31.data
Loading: [.]

Wir können auch die Datei an das Worksheet anhängen (Menüpunkt: Data -> Upload or create file...)
Mit DATA + dateiname kann man auf angehängte Dateien zugreifen:

datei = open(DATA + 'bsp31.data')
data = [map(float, line.split()) for line in datei.readlines()]
datei.close()

list_plot(data, rgbcolor = 'red')

var('a, b, c, varphi')

(a, b, c, varphi)

(a, b, c, varphi)

f(x) = a * exp(-b * sin(c * x + varphi))
show(f)

x \ {\mapsto}\ {a {e}^{-\left( {b \sin \left( {c x} + \varphi \right)} \right)} }

x \ {\mapsto}\ {a {e}^{-\left( {b \sin \left( {c x} + \varphi \right)} \right)} }

fit = find_fit(data, f, solution_dict = True)
fit

{a: 3.1493338629029637, c: 0.99864135059530146, b:
1.9550712343799732, varphi: 0.82005579657993377}

{a: 3.1493338629029637, c: 0.99864135059530146, b: 1.9550712343799732, varphi: 0.82005579657993377}

p1 = list_plot(data, rgbcolor = 'red')
p2 = plot(f(x).subs(fit), 0, 25)
p = p1 + p2
p.axes_labels(['$x$', '$f(x)$'])
show(p, ymax = 20, xmax = 23)

Beispiel 32

Die Newton-Iteration ist ein numerisches Verfahren zur näherungsweisen Berechnung von Nullstellen einer Funktion f. Sie ist definiert durch die rekursive Folge:

x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}

und einem Startwert x_0.

Schreiben Sie einen Generator newton(f, x0), der für eine gegebene Funktion f und dem Startwert x0, die Newton Iteration durchführt.

Schreiben Sie auch eine geeignete Abbruchbedingung für die Iteration.

Verwenden Sie Ihren Generator um eine Nullstelle von
f(x) = x^3 + 6 x^2+9 x+1
zu bestimmen. Verwenden Sie als Startwert x_0 = 0.
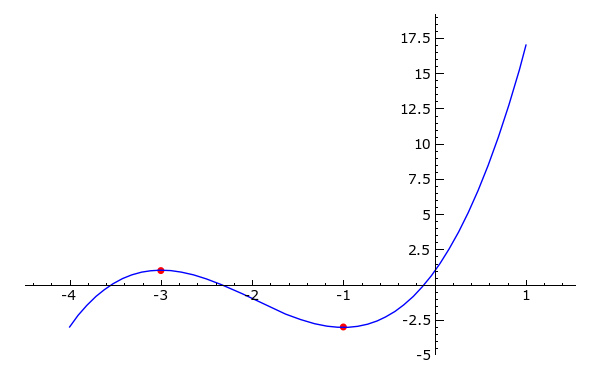
Verwenden Sie nun die folgenden Startwerte: -4,-3,-2,-1,0,1
Versuchen Sie anhand des Funktionsgraphen von f, das Verhalten des Newtonverfahrens für die verschiedenen Startwerte zu erklären.
Achtung: Die Newton-Iteration funktioniert vielleicht nicht für alle Startwerte.

def newton(f, x0):
f1 = f.diff()
xn = RDF(x0)
yield xn, f(xn)
while f(xn) != 0:
xn = xn - f(xn) / f1(xn)
yield xn, f(xn)

def take(g, n):
l = []
for i in xrange(n):
try:
l.append(g.next())
except StopIteration:
break
return l

f = x^3 + 6*x^2+9*x+1
show(f)

{x}^{3}  + {6 {x}^{2} } + {9 x} + 1

{x}^{3}  + {6 {x}^{2} } + {9 x} + 1

show(take(newton(f, 0), 5))

\begin{array}{l}[\left(0.0, 
 1.0\right),\\
\left(-0.111111111111, 
 0.0727023319616\right),\\
\left(-0.120548433048, 
 0.000503850073677\right),\\
\left(-0.120614755163, 
 2.4800704268 \times 10^{-08}\right),\\
\left(-0.120614758428, 
 3.33066907388 \times 10^{-16}\right)]\end{array}

\begin{array}{l}[\left(0.0, 
 1.0\right),\\
\left(-0.111111111111, 
 0.0727023319616\right),\\
\left(-0.120548433048, 
 0.000503850073677\right),\\
\left(-0.120614755163, 
 2.4800704268 \times 10^{-08}\right),\\
\left(-0.120614758428, 
 3.33066907388 \times 10^{-16}\right)]\end{array}

def newton_terminate(g, epsilon):
x, fx = g.next()
while abs(fx) > epsilon:
x, fx = g.next()
return x, fx

show([(x0, newton_terminate(newton(f, x0), 10^(-10))) for x0 in [-4..1]])

\begin{array}{l}[\left(-4, 
 \left(-3.53208888624, 
 -4.61852778244 \times 10^{-14}\right)\right),\\
\left(-3, 
 \left(-inf, 
 nan\right)\right),\\
\left(-2, 
 \left(-2.34729635533, 
 -1.06581410364 \times 10^{-14}\right)\right),\\
\left(-1, 
 \left(nan, 
 nan\right)\right),\\
\left(0, 
 \left(-0.120614758428, 
 3.33066907388 \times 10^{-16}\right)\right),\\
\left(1, 
 \left(-0.120614758428, 
 0.0\right)\right)]\end{array}

\begin{array}{l}[\left(-4, 
 \left(-3.53208888624, 
 -4.61852778244 \times 10^{-14}\right)\right),\\
\left(-3, 
 \left(-inf, 
 nan\right)\right),\\
\left(-2, 
 \left(-2.34729635533, 
 -1.06581410364 \times 10^{-14}\right)\right),\\
\left(-1, 
 \left(nan, 
 nan\right)\right),\\
\left(0, 
 \left(-0.120614758428, 
 3.33066907388 \times 10^{-16}\right)\right),\\
\left(1, 
 \left(-0.120614758428, 
 0.0\right)\right)]\end{array}

Die Nullstellen von f:

map(lambda x: n(x[0]), f.roots())

[-2.34729635533386, -3.53208888623796, -0.120614758428183]

[-2.34729635533386, -3.53208888623796, -0.120614758428183]

roots = f.derivative().roots()
roots

[(-3, 1), (-1, 1)]

[(-3, 1), (-1, 1)]

p = plot(f, -4, 1)
for x, mult in roots:
p += point((x, f(x)), rgbcolor = 'red', pointsize = 20)
show(p)

Beispiel 33

Schreiben Sie eine Funktion taylor_polynom(f, x, x0, n) die das Taylor Polynom vom Grad n der Funktion f(x) mit Entwicklungspunkt x0 berechnet.

Vergleichen Sie ihre Funktion anhand einiger selbstgewählter Beispiele mit der eingebauten Funktion taylor.
Stellen Sie sicher, dass taylor_polynom auch für Funktionen mit Parametern richtig funktioniert, und verwenden Sie sie um das Taylor Polynom vom Grad 10 mit dem Entwicklungspunkt x_0=0 für die Funktion
f(x) = \sin(a x)
zu berechnen.

def taylor_polynom(f, x, x0, n):
p = SR(0)
fdiff = f
for i in xrange(n+1):
p += fdiff(x=x0)*(x-x0)^i/factorial(i)
fdiff = diff(fdiff, x)
return p

var('x')
show(expand(taylor(sin(x)*cos(x/2), x, 0, 5)))

\frac{{61 {x}^{5} }}{1920} - \frac{{7 {x}^{3} }}{24} + x

\frac{{61 {x}^{5} }}{1920} - \frac{{7 {x}^{3} }}{24} + x

show(taylor_polynom(sin(x)*cos(x/2), x, 0, 5))

\frac{{61 {x}^{5} }}{1920} - \frac{{7 {x}^{3} }}{24} + x

\frac{{61 {x}^{5} }}{1920} - \frac{{7 {x}^{3} }}{24} + x

show(expand(taylor(log(x), x, 1, 5)))

\frac{{x}^{5} }{5} - \frac{{5 {x}^{4} }}{4} + \frac{{10 {x}^{3} }}{3} - {5 {x}^{2} } + {5 x} - \frac{137}{60}

\frac{{x}^{5} }{5} - \frac{{5 {x}^{4} }}{4} + \frac{{10 {x}^{3} }}{3} - {5 {x}^{2} } + {5 x} - \frac{137}{60}

show(expand(taylor_polynom(log(x), x, 1, 5)))

\frac{{x}^{5} }{5} - \frac{{5 {x}^{4} }}{4} + \frac{{10 {x}^{3} }}{3} - {5 {x}^{2} } + {5 x} - \frac{137}{60}

\frac{{x}^{5} }{5} - \frac{{5 {x}^{4} }}{4} + \frac{{10 {x}^{3} }}{3} - {5 {x}^{2} } + {5 x} - \frac{137}{60}

var('a,x')
show(expand(taylor_polynom(sin(a*x), x, 0, 10)))

\frac{{{a}^{9}  {x}^{9} }}{362880} - \frac{{{a}^{7}  {x}^{7} }}{5040} + \frac{{{a}^{5}  {x}^{5} }}{120} - \frac{{{a}^{3}  {x}^{3} }}{6} + {a x}

\frac{{{a}^{9}  {x}^{9} }}{362880} - \frac{{{a}^{7}  {x}^{7} }}{5040} + \frac{{{a}^{5}  {x}^{5} }}{120} - \frac{{{a}^{3}  {x}^{3} }}{6} + {a x}

show(expand(taylor(sin(a*x), x, 0, 10)))

\frac{{{a}^{9}  {x}^{9} }}{362880} - \frac{{{a}^{7}  {x}^{7} }}{5040} + \frac{{{a}^{5}  {x}^{5} }}{120} - \frac{{{a}^{3}  {x}^{3} }}{6} + {a x}

\frac{{{a}^{9}  {x}^{9} }}{362880} - \frac{{{a}^{7}  {x}^{7} }}{5040} + \frac{{{a}^{5}  {x}^{5} }}{120} - \frac{{{a}^{3}  {x}^{3} }}{6} + {a x}

f = sin(x)*cos(x/2)
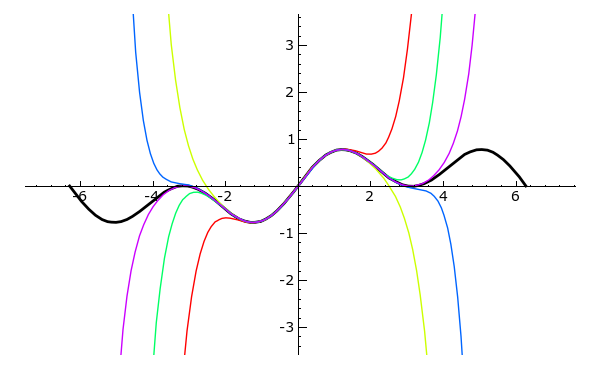
p = plot(f, -2*pi, 2*pi, color = 'black', thickness = 2)
colors = rainbow(10)
for i in xrange(5,15,2):
p += plot(taylor_polynom(f, x, 0, i), -2*pi, 2*pi, color = colors[i-5])
p.show(ymin=-3, ymax=3)