Beispiel 34-39

Computermathematik (für Informatik)

6. Übungsblatt
28. 1. 2009

Die heutigen Übungen sollen mit dem Computeralgebrasystem Sage gelöst werden.

Die Lösung der Beispiele soll auf möglichst kompakte Weise erfolgen. Wenn zum Beispiel eine Funktion für mehrere Werte berechnet werden soll, soll das mittels einer geeigneten Schleifen oder Listen Operation erfolgen, und nicht alle Werte einzeln eingetippt werden.

Zwischenergebnisse welche in einem weiteren Berechnungsschritt benötigt werden, sollen in eine Variable gespeichert und weiterverwendet werden (nicht neu eintippen).

Beispiel 34

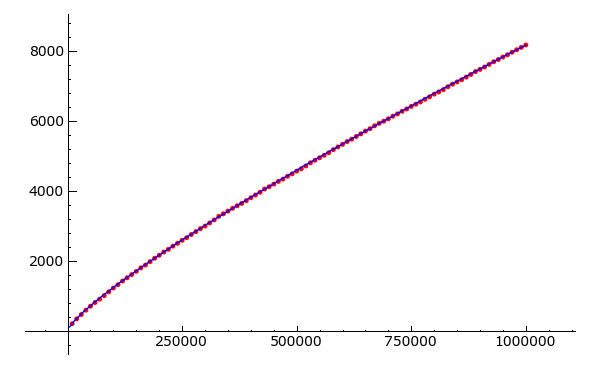
Eine Zahl p heisst Primzahlzwilling wenn p und p+2 Primzahlen sind. Es wird vermutet dass unendlich viele Primzahlzwillinge existieren. Allerdings konnte das noch niemand beweisen.

Sei

z(x) = |\lbrace p \leq x:\: p \text{ und } p + 2 \text{ sind Primzahlen}\rbrace|.
Also z(x) ist die Anzahl der Primzahlzwillinge die kleiner als x sind.

In numerischen Berechnungen wurde festgestellt, dass

z(x) \approx \frac{C\cdot x}{\ln(x)^\alpha}
mit reellen Konstanten C und \alpha.

Bestimmen Sie Werte von z(x) für mindestens x\leq 10^6 und schätzen Sie daraus plausible Werte für die Konstanten C und \alpha.

Hinweis: Verwenden Sie die Funktion find_fit. Sie finden diese Funktion in Datei find_fit.sage auf der Homepage der Vorlesung.

def z(x):
   return len([p for p in xrange(x) if is_prime(p) and is_prime(p+2)]) 
       
def z(x, n = 100):
   data = []
   np = 1
   prime_twins = 0
   xi = x / n
   while np <= x:
       np = next_prime(np)
       if np > xi:
           data.append((xi, prime_twins))
           xi += x / n
       if is_prime(np + 2):
           prime_twins += 1

   return data 
       
def z(x, n = 100):
   prime_twins = [p for p in xrange(x) if is_prime(p) and is_prime(p+2)]
   data = []

   for i in [1..n]:
     xi = i * x / n
     if xi <= 2:
       continue
     data.append((xi, len(filter(lambda x: x <= xi, prime_twins))))
   return data 
       
time data = z(10^6) 
        
CPU time: 6.41 s,  Wall time: 6.47 s
CPU time: 6.41 s,  Wall time: 6.47 s
var('C, alpha')
model(x) = C * x / log(x)^alpha
show(model) 
        
x \ {\mapsto}\ \frac{{x C}}{{\log \left( x \right)}^{\alpha} }
x \ {\mapsto}\ \frac{{x C}}{{\log \left( x \right)}^{\alpha} }
load find_fit.sage 
       
sol = find_fit(data, model, solution_dict = True)
sol 
        
{alpha: 2.2339162678491307, C: 2.8791212176199901}
{alpha: 2.2339162678491307, C: 2.8791212176199901}
list_plot(data, rgbcolor = 'red') + plot(model(x).subs(sol), 1, 10^6) 
       

Beispiel 35

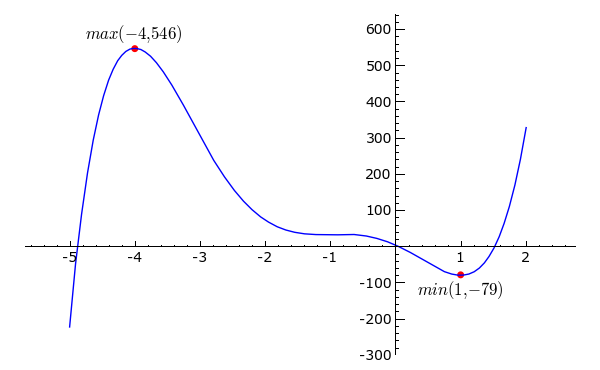
Finden Sie sämtliche Extremwerte (lokale Maxima und Minima) der Funktion

f(x) = 4x^5 + 25x^4 + 20x^3 - 50x^2 - 80x + 2.

Zeichnen Sie die Extremwerte in den Graphen der Funktion f ein, und beschriften Sie sie mit ihren Koordinaten.

Hinweis: Verwenden Sie die Funktion text.

P.<x> = QQ[]
f = 4*x^5 + 25*x^4+20*x^3-50*x^2-80*x+2
show(f) 
        
4 x^{5} + 25 x^{4} + 20 x^{3} - 50 x^{2} - 80 x + 2
4 x^{5} + 25 x^{4} + 20 x^{3} - 50 x^{2} - 80 x + 2
f1 = f.derivative()
f2 = f1.derivative()
show(f1)
show(f2) 
        
20 x^{4} + 100 x^{3} + 60 x^{2} - 100 x - 80


80 x^{3} + 300 x^{2} + 120 x - 100
20 x^{4} + 100 x^{3} + 60 x^{2} - 100 x - 80


80 x^{3} + 300 x^{2} + 120 x - 100
extrema_kandidaten = set([e for (e, mult) in f1.roots()])
extrema_kandidaten 
        
set([1, -4, -1])
set([1, -4, -1])
wendepunkte = set([e for (e, mult) in f2.roots()])
wendepunkte 
        
set([-1])
set([-1])
extrema = list(extrema_kandidaten.difference(wendepunkte))
extrema = [(e, f(e)) for e in extrema]
extrema 
        
[(1, -79), (-4, 546)]
[(1, -79), (-4, 546)]
g = plot(f, -5, 2)
g += points(extrema, rgbcolor = 'red', pointsize = 20)
minx, miny = extrema[0]
maxx, maxy = extrema[1]
fontopts = {'rgbcolor': 'black', 'fontsize': 12}
g += text('$min(%d,%d)$' % (minx, miny), (minx, miny-10), vertical_alignment = 'top', **fontopts)
g += text('$max(%d,%d)$' % (maxx, maxy), (maxx, maxy+10), vertical_alignment = 'bottom', **fontopts)
g.show() 
       

Beispiel 36

Finden Sie alle stationären Punkte der Funktion

f(x, y) = -3 x^3-2 (y-1) x+y^3+1,

und visualisieren Sie ihr Ergebnis.

Hinweis: plot3d, point3d

f(x, y) = -3*x^3-2*(y-1)*x+y^3+1
show(f) 
        
\left(x, y \right)\ {\mapsto}\ {y}^{3}  - {{2 x} \left( y - 1 \right)} - {3 {x}^{3} } + 1
\left(x, y \right)\ {\mapsto}\ {y}^{3}  - {{2 x} \left( y - 1 \right)} - {3 {x}^{3} } + 1
fx = diff(f, x)
fy = diff(f, y)
show(fx)
show(fy) 
        
\left(x, y \right)\ {\mapsto}\ {-2 \left( y - 1 \right)} - {9 {x}^{2} }


\left(x, y \right)\ {\mapsto}\ {3 {y}^{2} } - {2 x}
\left(x, y \right)\ {\mapsto}\ {-2 \left( y - 1 \right)} - {9 {x}^{2} }


\left(x, y \right)\ {\mapsto}\ {3 {y}^{2} } - {2 x}
sol = solve([fx == 0, fy == 0], [x, y], solution_dict = True)
sol 
        
[{y: 0.476783859961, x: 0.34098424431}, {y: 0.566281460574*I +
0.0785070528727, x: 0.133371265698*I - 0.471767002859}, {y:
0.0785070528727 - 0.566281460574*I, x: -0.133371265698*I -
0.471767002859}, {y: -0.633797909408, x: 0.602549765153}]
[{y: 0.476783859961, x: 0.34098424431}, {y: 0.566281460574*I + 0.0785070528727, x: 0.133371265698*I - 0.471767002859}, {y: 0.0785070528727 - 0.566281460574*I, x: -0.133371265698*I - 0.471767002859}, {y: -0.633797909408, x: 0.602549765153}]
real_solutions = filter(lambda s: s[x].imag() == 0 and s[y].imag() == 0, sol)
real_solutions 
        
[{y: 0.476783859961, x: 0.34098424431}, {y: -0.633797909408, x:
0.602549765153}]
[{y: 0.476783859961, x: 0.34098424431}, {y: -0.633797909408, x: 0.602549765153}]
[f.subs(s) for s in real_solutions] 
        
[1.34626181073, 2.05799621029]
[1.34626181073, 2.05799621029]
G = plot3d(f, (x,-1,1), (y, -1,1))
fs = [lambda x,y: f.subs(s) for s in real_solutions]
colors = ['red', 'green']
for i, s in enumerate(real_solutions):
   if s[x].imag() == 0 and s[y].imag() == 0:
       html("$E_%d = (%2.2f, %2.2f, %2.2f)" % (i, s[x], s[y], float(f.subs(s))) )
       G += point3d((s[x],s[y], f.subs(s)), color = 'red')
       G += plot3d(fs[i](x,y), (x,s[x]-0.5,s[x]+0.5), (y,s[y]-0.5,s[y]+0.5), color = colors[i], opacity = 0.5)
       G += text3d("S%d" %i, (s[x],s[y], f.subs(s)+0.1))
G.show() 
        
E_0 = (0.34, 0.48, 1.35)
E_1 = (0.60, -0.63, 2.06)
E_0 = (0.34, 0.48, 1.35)
E_1 = (0.60, -0.63, 2.06)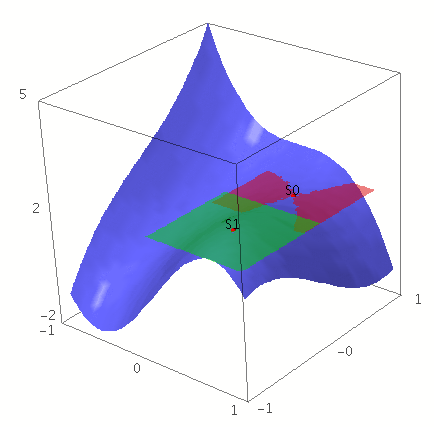

Beispiel 38

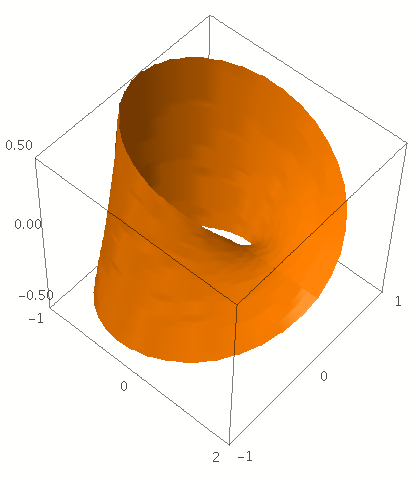
Ein Möbius-Band hat die Parameterdarstellung:


\begin{align*}
x(r, \alpha) &= \cos(\alpha) \cdot \left(1+\frac{r}{2}\cos\frac{\alpha}{2}\right) \\
y(r, \alpha) &= \sin(\alpha) \cdot \left(1+\frac{r}{2}\cos\frac{\alpha}{2}\right) \\
z(r, \alpha) &= \frac{r}{2} \sin\frac{\alpha}{2}
\end{align*}

mit den Parametern 0\leq \alpha < 2\pi und -1\leq r \leq 1.

Zeichnen Sie das Möbiusband in 3D.

var('r, alpha')
x = cos(alpha) * (1 + r/2 * cos(alpha/2))
y = sin(alpha) * (1 + r/2 * cos(alpha/2))
z = r/2 * sin(alpha/2) 
       
parametric_plot3d((x, y, z), (alpha, 0, 2*pi), (r, -1, 1), color = 'orange') 
       

Beispiel 39

Die Monte-Carlo Methode ist eine näherungsweise Methode zur Berechnung von \pi. Dabei wird eine Folge von n zufällig verteilten Punkten im Einheitsquadrat erzeugt. Für jeden dieser Punkte wird überprüft, ob er in einem in dieses Quadrat eingeschriebenen Viertelkreis liegt. Für großes n ist der Anteil der im Viertelkreis liegenden Punkten dann ungefähr \frac{\pi}{4}.

Die folgende Skizze soll das Verfahren verdeutlichen:

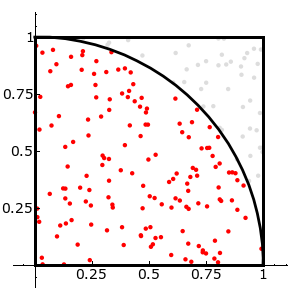
\frac{\mbox{Anzahl der roten Punkte}}{\mbox{Anzahl aller Punkte}} \approx \frac{\pi}{4}

Implementieren Sie dieses Verfahren zur Approximation von \pi.

def piapprox_animate(frames, n):
   f = lambda x: sqrt(1-x^2)
   pi_list = []
   notpi_list = []
   g_list = []
   for k in range(1, frames+1):
       for i in range(n):
           xp = random()
           yp = random()
           if yp <= f(xp):
               pi_list.append((xp, yp))
           else:
               notpi_list.append((xp, yp))

       pi_approx = 4*len(pi_list)/(k*n)

       g = plot(f, 0,1, color = 'black', thickness = 2)
       g += text('$\\pi\\approx %.3f$' % pi_approx, (0.5, 1.05), rgbcolor = 'black', fontsize = 20)
       g += line([(0,0), (0,1), (1,1), (1,0), (0,0)], rgbcolor = 'black', thickness = 2)
       g += points(pi_list, rgbcolor = 'red', pointsize = 2)
       g += points(notpi_list, rgbcolor = '#ddd', pointsize = 2)
       g.set_aspect_ratio(1)
       g_list.append(g)

   return g_list 
       
a = animate(piapprox_animate(20, 2000)) 
       
a.show(delay = 100) 
       
def pi_monte_carlo(n):
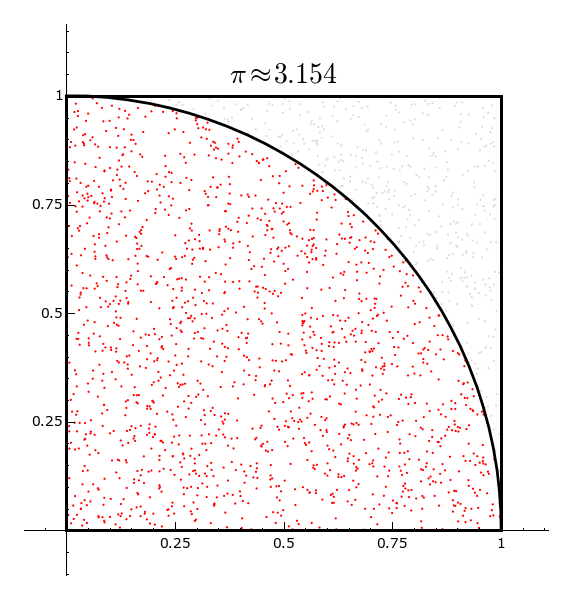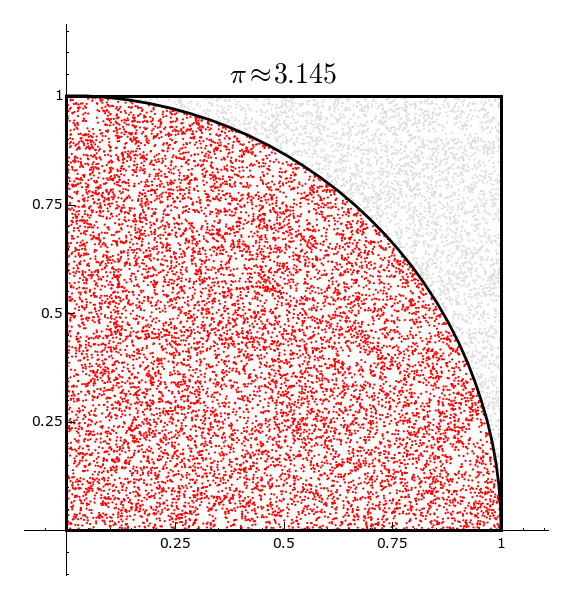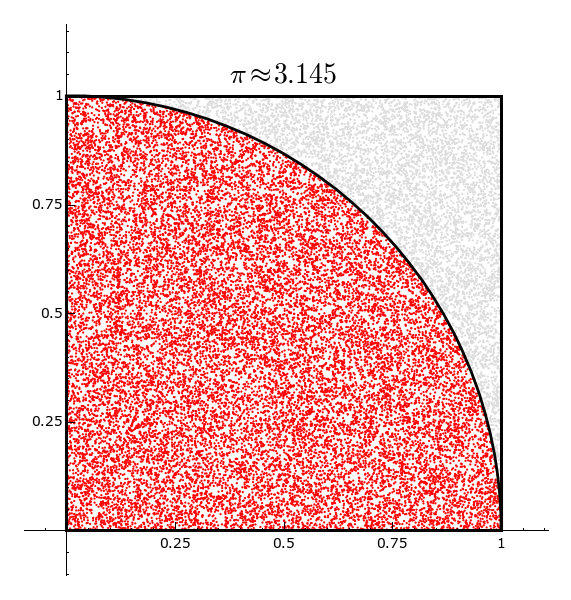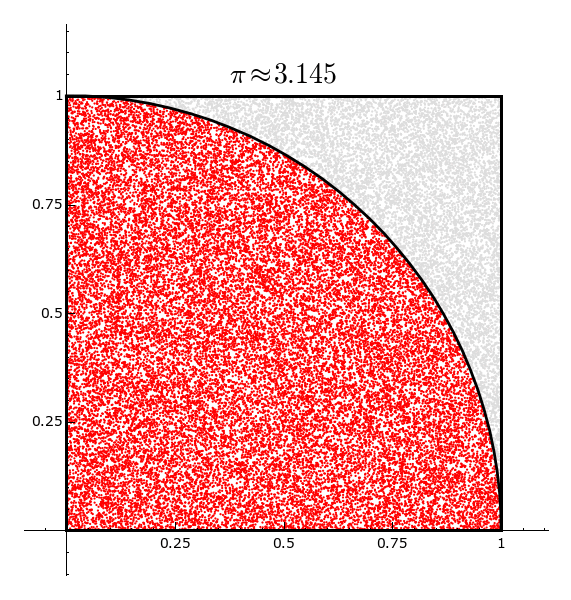   f = lambda x: sqrt(1-x^2)
   pi_count = 0
   for i in xrange(n):
       xp = random()
       yp = random()
       if yp <= f(xp):
           pi_count += 1

   pi_approx = 4*pi_count/n
   return pi_approx 
       
time pi_approx = pi_monte_carlo(10^6)
html('$\\pi\\approx %.4f$' % pi_approx) 
        
Time: CPU 32.04 s, Wall: 32.54 s
\pi\approx 3.1395
Time: CPU 32.04 s, Wall: 32.54 s
\pi\approx 3.1395