Sage Tutorium 1

Inhaltsverzeichnis

  1. Sage als Taschenrechner
  2. Symbolisches Rechnen
  3. Plotten von Funktionen
  4. Interaktive Programme
  5. Kontrollstrukturen
  6. Definieren von Funktionen

Sage als Taschenrechner

Man kann Sage einfach als sehr mächtigen Taschenrechner verwenden. Es werden dabei Zahlen mit beliebiger Genauigkeit unterstützt, ebenso Brüche und komplexe Zahlen. Für viele Berechnungen werden exakte Ergebnisse geliefert.

Um eine Rechnung auszuführen, geben wir die Rechnung in eine Zelle ein und drücken dann Umschalt + Enter um die Berechnung zu starten.

1 + 1 
        
2
2
(2 * 2 + 5)/3 
        
3
3

Exponentation

2^10 
        
1024
1024

Langzahlarithmetik

2^1000 
        
10715086071862673209484250490600018105614048117055336074437503883703\
51051124936122493198378815695858127594672917553146825187145285692314\
04359845775746985748039345677748242309854210746050623711418779541821\
53046474983581941267398767559165543946077062914571196477686542167660\
429831652624386837205668069376
10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376

Bruchrechnen

1/6 + 7/12 
        
3/4
3/4

Komplexe Zahlen

sqrt(-4) 
        
2*I
2*I
I^2 
        
-1
-1
Realteil
real((1 + I)/(1 - I)) 
        
0
0
Imaginärteil
imag((1 + I)/(1 - I)) 
        
1
1

Exakte Auswertung mathematischer Funktionen

sin(pi/2) 
        
1
1
sin(pi/3) 
        
sqrt(3)/2
sqrt(3)/2
sin(pi/4) 
        
1/sqrt(2)
1/sqrt(2)
Um Ungeleichungen exakt auszuwerten, müssen wir sie in einen Wahrheitswert umwandeln.
bool(sqrt(2) < 2 * sin(pi/3)) 
        
True
True

Gleitkommaarithmetik mit beliebiger Genauigkeit

numerical_approx(pi, digits = 400) 
        
3.141592653589793238462643383279502884197169399375105820974944592307\
81640628620899862803482534211706798214808651328230664709384460955058\
22317253594081284811174502841027019385211055596446229489549303819644\
28810975665933446128475648233786783165271201909145648566923460348610\
45432664821339360726024914127372458700660631558817488152092096282925\
4091715364367892590360011330530548820466521384146951941511609
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609
Dasselbe in objektorientierter Notation
(pi + e^2).n(digits = 1000) 
        
10.53064875252044346569307084385451069737748496992695314506207241483\
03902023652667620123473104212388627559012477787611727709784483023318\
55606203751621526558892350406998309349274807950975570499637016963784\
69845884387433766711073088310952924570668588183727498045499422364962\
97922263889433805673555524487890454058302910103812047950796924085123\
78014988128970480930356472543379834030145426522971615928634423159918\
33510138597124827441396033036719792839281241506021438151270971542695\
77240182606467901802408317660896453035365228345658928992747929180018\
00937296173333692781053000583057675416277360434289533620709249060138\
33879518199973750309002758643851883702926331707287258181290037567515\
93546118974294829403738196647637551141261429810903623516013132460565\
86458328420673854140233615136790889727986004386488963891429010084124\
90961373517244673668998768162507274864289812079578153923518660991290\
85399901363931432906715643053900085785017530929629326834686691730486\
59484089104656230634485278072743356252407955007914689151500640009453\
0027
10.5306487525204434656930708438545106973774849699269531450620724148303902023652667620123473104212388627559012477787611727709784483023318556062037516215265588923504069983093492748079509755704996370169637846984588438743376671107308831095292457066858818372749804549942236496297922263889433805673555524487890454058302910103812047950796924085123780149881289704809303564725433798340301454265229716159286344231599183351013859712482744139603303671979283928124150602143815127097154269577240182606467901802408317660896453035365228345658928992747929180018009372961733336927810530005830576754162773604342895336207092490601383387951819997375030900275864385188370292633170728725818129003756751593546118974294829403738196647637551141261429810903623516013132460565864583284206738541402336151367908897279860043864889638914290100841249096137351724467366899876816250727486428981207957815392351866099129085399901363931432906715643053900085785017530929629326834686691730486594840891046562306344852780727433562524079550079146891515006400094530027
Bei längeren Berechnungen ist es sinnvoll sich zuerst einen geeigneten Datentyp zu definieren.
a = R(pi + 2 * cos(sqrt(2))) # ist aequivalent zu a = (pi + 2*cos(sqrt(2))).n(prec=1000)
a 
        
3.453480043120542185371939341096682167446063900157716534755765127785\
81944853927991583839488586037872127640744221244934330297809724069799\
19670147290414122985134570460403690116304829310315448867242399467850\
77610792415740531848854966254982524545236646057277418278878175995282\
69501839305499660252464797407
3.45348004312054218537193934109668216744606390015771653475576512778581944853927991583839488586037872127640744221244934330297809724069799196701472904141229851345704604036901163048293103154488672423994678507761079241574053184885496625498252454523664605727741827887817599528269501839305499660252464797407
type(a) 
        
<type 'sage.rings.real_mpfr.RealNumber'>
<type 'sage.rings.real_mpfr.RealNumber'>
parent(a) 
        
Real Field with 1000 bits of precision
Real Field with 1000 bits of precision
Achtung: Kommen Zahlen unterschiedlicher Präzision in einer Rechnung vor, dann hat das Ergebnis immer die kleinste Präzision. Konstanten müssen also manuell zu einer Zahl mit hoher Präzision konvertiert werden.
parent(0.1) 
        
Real Field with 53 bits of precision
Real Field with 53 bits of precision
Falsch:
a1 = 2 * a + 0.1
a1; parent(a1) 
        
7.00696008624108
Real Field with 53 bits of precision
7.00696008624108
Real Field with 53 bits of precision
Falsch: Hier wird mit 2a+0.1 mit niedriger Präzision berechnet, und danach das Ergebnis zu einer Zahl mit 1000 Bit Präzision konvertiert
b = R(2 * a + 0.1)
b; parent(b) 
        
7.006960086241083907054871815489605069160461425781250000000000000000\
00000000000000000000000000000000000000000000000000000000000000000000\
00000000000000000000000000000000000000000000000000000000000000000000\
00000000000000000000000000000000000000000000000000000000000000000000\
00000000000000000000000000000
Real Field with 1000 bits of precision
7.00696008624108390705487181548960506916046142578125000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Real Field with 1000 bits of precision
Richtig:
c = 2 * a + R(0.1)
c; parent(c) 
        
7.006960086241084370743878682193364334892127800315433069511530255571\
63889707855983167678977172075744255281488442489868660595619448139598\
39340294580828245970269140920807380232609658620630897734484798935701\
55221584831481063697709932509965049090473292114554836557756351990565\
39003678610999320504929594815
Real Field with 1000 bits of precision
7.00696008624108437074387868219336433489212780031543306951153025557163889707855983167678977172075744255281488442489868660595619448139598393402945808282459702691409208073802326096586206308977344847989357015522158483148106369770993250996504909047329211455483655775635199056539003678610999320504929594815
Real Field with 1000 bits of precision

Symbolisches Rechnen

Symbolische Variablen müssen deklariert werden.
var('x, y, z') 
        
(x, y, z)
(x, y, z)
expr1 = (x + y + z)^3
expr1 
        
(z + y + x)^3
(z + y + x)^3
type(expr1); parent(expr1) 
        
<class 'sage.calculus.calculus.SymbolicArithmetic'>
Symbolic Ring
<class 'sage.calculus.calculus.SymbolicArithmetic'>
Symbolic Ring
Anzeige in mathematischer Notation
view(expr1) 
        
(z+y+x)3 
(z+y+x)3 
Ausmultiplizieren
view(expand(expr1)) 
        
z3+3yz2+3xz2+3y2z+6xyz+3x2z+y3+3xy2+3x2y+x3 
z3+3yz2+3xz2+3y2z+6xyz+3x2z+y3+3xy2+3x2y+x3 
Faktorisieren
expr2 = (x^2 - 2 * x * y + y^2)
view(expr2) 
        
y2−2xy+x2 
y2−2xy+x2 
view(factor(expr2)) 
        
(x−y)2
(x−y)2
Substitution von Variablen und Termen
expr3 = expr2(y = sin(z^2))
view(expr3) 
        
(sin(z2))2−2xsin(z2)+x2 
(sin(z2))2−2xsin(z2)+x2 
expr3.subs_expr(sin(z^2) == y) 
        
y^2 - 2*x*y + x^2
y^2 - 2*x*y + x^2
Differentialrechnung
diff(x * sin(x), x) 
        
sin(x) + x*cos(x)
sin(x) + x*cos(x)

Polynome

Wir konstruieren einen Datentyp für Polynome in der Variablen t, und Koeffizienten aus den Rationalen Zahlen (Q).
P.<t> = QQ[]
type(P) 
        
<class
'sage.rings.polynomial.polynomial_ring.PolynomialRing_field'>
<class 'sage.rings.polynomial.polynomial_ring.PolynomialRing_field'>
gen() gibt die Variable des Polynoms zurück.
P.gen() 
        
t
t
Wir definieren uns einige Polynome
p1 = (1/2 * t - 3/2) * (t - 1/4)
view(p1) 
        
21t2−813t+83 
21t2−813t+83 
roots() berechnet die Nullstellen eines Polynoms zusammen mit ihren Vielfachheiten.
p1.roots() 
        
[(3, 1), (1/4, 1)]
[(3, 1), (1/4, 1)]
Probe durch Einsetzen.
p1(3); p1(1/4) 
        
0
0
0
0
degree() berechnet den Grad des Polynoms.
p1.degree() 
        
2
2
p2 = (1 + t - t^2)^3
view(p2) 
        
−t6+3t5−5t3+3t+1 
−t6+3t5−5t3+3t+1 
parent(p2) 
        
Univariate Polynomial Ring in t over Rational Field
Univariate Polynomial Ring in t over Rational Field
Standardmäßig berechnet roots() nur Nullstellen in der selben Grundmenge in der die Koeffizienten des Polynoms liegen. In unserem Fall Q. Unser Polynom hat keine rationalen Nullstellen.
p2.roots() 
        
[]
[]
Wir können die Grundmenge aber auch explizit angeben. Hier berechnen wir alle reellen Nullstellen.
p2.roots(ring = RR) 
        
[(-0.618031057174341, 1), (1.61804465415111, 1)]
[(-0.618031057174341, 1), (1.61804465415111, 1)]
Um sämtliche Nullstellen zu bekommen, brauchen wir komplexe Zahlen.
p2.roots(ring = CC) 
        
[(-0.618031057174341, 1), (1.61804465415111, 1), (1.61802865604929 +
9.23641138258941e-6*I, 1), (1.61802865604929 -
9.23641138258941e-6*I, 1), (-0.618035454537672 +
2.53887260392275e-6*I, 1), (-0.618035454537672 -
2.53887260392275e-6*I, 1)]
[(-0.618031057174341, 1), (1.61804465415111, 1), (1.61802865604929 + 9.23641138258941e-6*I, 1), (1.61802865604929 - 9.23641138258941e-6*I, 1), (-0.618035454537672 + 2.53887260392275e-6*I, 1), (-0.618035454537672 - 2.53887260392275e-6*I, 1)]

Plotten von Funktionen

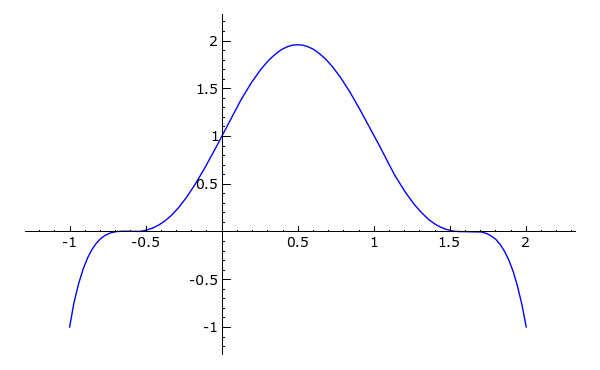
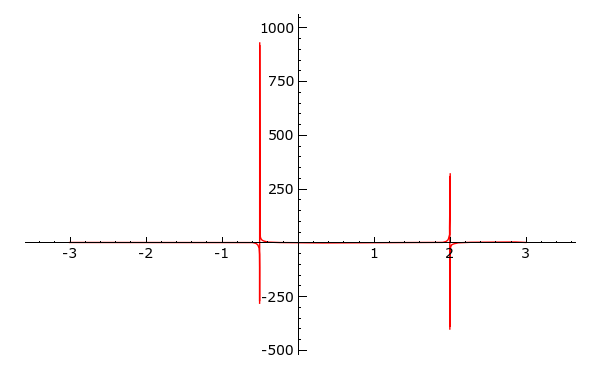
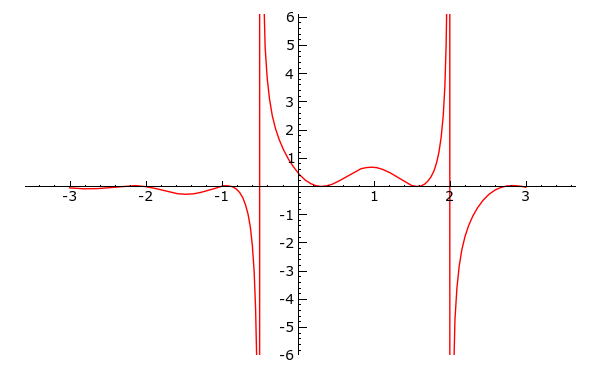
Sage verfügt über vielfältige High-level Funktionen zum Plotten von Funktionen.

Wir plotten das Polynom p2=−t6+3t5−5t3+3t+1 im Interval [−1,2].

plot(p2, -1, 2) 
       
Plot einer Funktion mit Polstellen. Es sind leider keine Details sichtbar.
Für ein besseres Ergebnis müssen wir den den Ausschnitt explizit auswählen.

Interaktive Programme

Sage bietet die Möglichkeit kleine interaktive Progamme in das Notebook einzubinden (Siehe die Dokumentation zu interact). Weitere Beispiele für interact finden im Sage-Wiki.

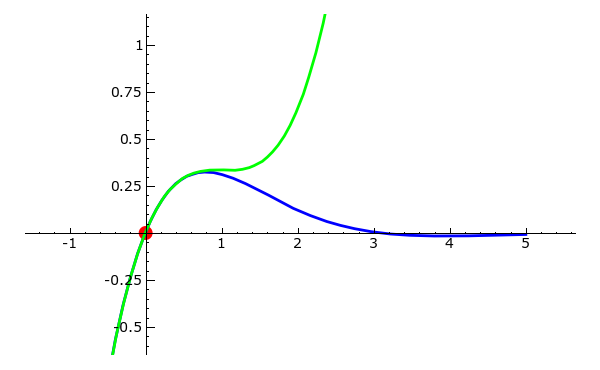
Das folgende Beispiel visualisiert die Taylorpolynome der Funktion f(x)=sin(x)·e−x.

var('x')
f = sin(x) * e^(-x)
p = plot(f, -1, 5, thickness = 2)
html('<h2>Taylor Polynome</h2>')

@interact
def _(x0 = input_box(0, label = "x0="),
     order = slider(0, 12, 1, label = "Ordnung: ", default = 3)):

   ft = f.taylor(x, x0, order)
   pt = plot(ft, -1, 5, color = 'green', thickness = 2)
   dot = point((x0, f(x0)), pointsize = 80, rgbcolor = (1, 0, 0))
   html('$f(x) = %s$' % latex(f))
   html('$\hat{f}(x;%s) = %s + \mathcal{O}(x^{%s})$' % (latex(x0), latex(ft), order + 1))
   (dot + p + pt).show(ymin = -.5, ymax = 1) 
       

Taylor Polynome
x0= 
Ordnung:  
f(x)=e−xsin(x) 
fˆ(x;0)=x−x2+3x3+O(x4)
CPU time: 0.04 s, Wall time: 0.11 s

Click to the left again to hide and once more to show the dynamic interactive window

Datentypen

Die wichtigsten Datentypen in Sage/Python sind:

Tupel

Tupel sind ähnlich wie Listen, nur können einmal erstellte Tupel nicht mehr verändert werden (immutable). Tupel sind besonders nützlich, um mehrere Werte gleichzeitig von einer Funktion zurückzugeben.

a = 1, 2, 3
a; type(a) 
        
(1, 2, 3)
<type 'tuple'>
(1, 2, 3)
<type 'tuple'>
a[0]; a[1]; a[2] 
        
1
2
3
1
2
3

Die Funktion xgcd(a, b) berechnet den kleinsten gemeinsamen Teiler von a und b mit Hilfe des erweiterten Euclidschen Algrithmus und gibt das Ergebnis als Tupel von drei Zahlen zurück.

t = xgcd(14, 25)
t 
        
(1, -16, 9)
(1, -16, 9)
Man kann die Elemente des Tupels auch direkt einzelnen Variablen zuweisen (Tupel unpacking).
a1, a2, a3 = xgcd(14, 25)
a2 
        
-16
-16
Simultanes vertauschen zweier Variablen
t1 = 10
t2 = cos(x)
t1; t2 
        
10
cos(x)
10
cos(x)
t1, t2 = t2, t1

t1; t2 
        
cos(x)
10
cos(x)
10

Listen

Listen sind wahrscheinlich der wichtigste Datentyp in Sage/Python. Der wichtigste Unterschied zu Tupeln ist dass Listen veränderbar (mutable) sind. Sie können Elemente zu Listen hinzufügen, löschen, verändern. Das ist bei Tupeln nicht möglich.

Einige Operationen auf Listen:

L = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
L 
        
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
len(L) 
        
10
10
Hinzufügen von Elementen
L.append(11)
print "Liste:", L
print "Anzahl der Elemente:", len(L) 
        
Liste: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
Anzahl der Elemente: 11
Liste: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
Anzahl der Elemente: 11
Ersetzen von Elementen und Teillisten
L[0] = "Hallo"
L 
        
['Hallo', 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
['Hallo', 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
L[1:3] = 1/2
L 
        
['Hallo', 1/2, 4, 5, 6, 7, 8, 9, 10, 11]
['Hallo', 1/2, 4, 5, 6, 7, 8, 9, 10, 11]
L[2] = [pi^2/6, e]
L 
        
['Hallo', 1/2, [pi^2/6, e], 5, 6, 7, 8, 9, 10, 11]
['Hallo', 1/2, [pi^2/6, e], 5, 6, 7, 8, 9, 10, 11]
Sehr nützlich ist die Funktion zip, die ein Tupel von Listen in eine Liste von Tupeln verwandelt.
zip([1, 2, 3], ['a', 'b', 'c'], [sin, cos, tan]) 
        
[(1, 'a', sin), (2, 'b', cos), (3, 'c', tan)]
[(1, 'a', sin), (2, 'b', cos), (3, 'c', tan)]

Erzeugen von Listen

range(10) 
        
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
range(0, 101, 20) 
        
[0, 20, 40, 60, 80, 100]
[0, 20, 40, 60, 80, 100]
range(10, 0, -1) 
        
[10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
[10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
srange ist ähnlich wie range, aber für Fließkommazahlen
srange(0, 1, 0.1, include_endpoint = True) 
        
[0.000000000000000, 0.100000000000000, 0.200000000000000,
0.300000000000000, 0.400000000000000, 0.500000000000000,
0.600000000000000, 0.700000000000000, 0.800000000000000,
0.900000000000000, 1.00000000000000]
[0.000000000000000, 0.100000000000000, 0.200000000000000, 0.300000000000000, 0.400000000000000, 0.500000000000000, 0.600000000000000, 0.700000000000000, 0.800000000000000, 0.900000000000000, 1.00000000000000]
R = RealField(prec = 200)
srange(R(0), R(0.5), R(0.1)) 
        
[0.00000000000000000000000000000000000000000000000000000000000,
0.10000000000000000000000000000000000000000000000000000000000,
0.20000000000000000000000000000000000000000000000000000000000,
0.30000000000000000000000000000000000000000000000000000000000,
0.40000000000000000000000000000000000000000000000000000000000]
[0.00000000000000000000000000000000000000000000000000000000000, 0.10000000000000000000000000000000000000000000000000000000000, 0.20000000000000000000000000000000000000000000000000000000000, 0.30000000000000000000000000000000000000000000000000000000000, 0.40000000000000000000000000000000000000000000000000000000000]

Kurznotation für Arithmetische Progressionen

Achtung: Diese Notation ist Sage spezifisch und funktioniert nicht in standard Python.
[1..100] 
        
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19,
20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36,
37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53,
54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70,
71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87,
88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100]
[1,3..10] 
        
[1, 3, 5, 7, 9]
[1, 3, 5, 7, 9]
[0,0.2..1] 
        
[0.000000000000000, 0.200000000000000, 0.400000000000000,
0.600000000000000, 0.800000000000000, 1.00000000000000]
[0.000000000000000, 0.200000000000000, 0.400000000000000, 0.600000000000000, 0.800000000000000, 1.00000000000000]

List Comprehensions

List Comprehensions orientieren sich an mathematischer Mengenschreibweise, und sind eine Elegante Art um komplexe Listen zu generieren.

[x^2 for x in range(10)] 
        
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
var('x')
[sin(x).diff(i) for i in [0..4]] 
        
[sin(x), cos(x), -sin(x), -cos(x), sin(x)]
[sin(x), cos(x), -sin(x), -cos(x), sin(x)]
[x^2 for x in [1..20] if x % 2 == 0] 
        
[4, 16, 36, 64, 100, 144, 196, 256, 324, 400]
[4, 16, 36, 64, 100, 144, 196, 256, 324, 400]
[(x,y) for x in [-3..3] for y in [-2..2] if -1 <= x-y <= 1] 
        
[(-3, -2), (-2, -2), (-2, -1), (-1, -2), (-1, -1), (-1, 0), (0, -1),
(0, 0), (0, 1), (1, 0), (1, 1), (1, 2), (2, 1), (2, 2), (3, 2)]
[(-3, -2), (-2, -2), (-2, -1), (-1, -2), (-1, -1), (-1, 0), (0, -1), (0, 0), (0, 1), (1, 0), (1, 1), (1, 2), (2, 1), (2, 2), (3, 2)]

Strings

Strings sind im wesentlichen Listen von Buchstaben, allerdings sind Strings aus Performencegründen nicht mutable, genauso wie Tupel.
s4 = s1.capitalize() + s2
s4 
        
'Computermathematik'
'Computermathematik'
s = s4 + " (%s)" % s3.capitalize()
s 
        
'Computermathematik (Informatik)'
'Computermathematik (Informatik)'
len(s) 
        
31
31
s[8:18].capitalize() 
        
'Mathematik'
'Mathematik'
s.split() 
        
['Computermathematik', '(Informatik)']
['Computermathematik', '(Informatik)']
s.upper() 
        
'COMPUTERMATHEMATIK (INFORMATIK)'
'COMPUTERMATHEMATIK (INFORMATIK)'
s[istart:istart + len(suchstring)] 
        
'Informatik'
'Informatik'

Dictionaries

Ein Dictionary speichert Zuordnungen von je einem Wert zu einem Schlüsselwert

Einige nützliche Funktionen:
huss = {'name': 'Wilfried Huss', 'office': 'C305', 'email': 'huss@finanz.math.tugraz.at'}
huss 
        
{'name': 'Wilfried Huss', 'office': 'C305', 'email':
'huss@finanz.math.tugraz.at'}
{'name': 'Wilfried Huss', 'office': 'C305', 'email': 'huss@finanz.math.tugraz.at'}
huss['name'] 
        
'Wilfried Huss'
'Wilfried Huss'
huss.keys() 
        
['name', 'office', 'email']
['name', 'office', 'email']
huss.values() 
        
['Wilfried Huss', 'C305', 'huss@finanz.math.tugraz.at']
['Wilfried Huss', 'C305', 'huss@finanz.math.tugraz.at']
huss.items() 
        
[('name', 'Wilfried Huss'), ('office', 'C305'), ('email',
'huss@finanz.math.tugraz.at')]
[('name', 'Wilfried Huss'), ('office', 'C305'), ('email', 'huss@finanz.math.tugraz.at')]
huss.has_key('name'), huss.has_key('nachname') 
        
(True, False)
(True, False)
for (key, value) in huss.iteritems():
 print key, ":", value 
        
name : Wilfried Huss
office : C305
email : huss@finanz.math.tugraz.at
name : Wilfried Huss
office : C305
email : huss@finanz.math.tugraz.at
primzahlen = {}
p = 1;
for i in [1..30]:
 p = next_prime(p)
 primzahlen[p] = i

primzahlen 
        
{2: 1, 3: 2, 5: 3, 7: 4, 11: 5, 13: 6, 17: 7, 19: 8, 23: 9, 29: 10,
31: 11, 37: 12, 41: 13, 43: 14, 47: 15, 53: 16, 59: 17, 61: 18, 67:
19, 71: 20, 73: 21, 79: 22, 83: 23, 89: 24, 97: 25, 101: 26, 103:
27, 107: 28, 109: 29, 113: 30}
{2: 1, 3: 2, 5: 3, 7: 4, 11: 5, 13: 6, 17: 7, 19: 8, 23: 9, 29: 10, 31: 11, 37: 12, 41: 13, 43: 14, 47: 15, 53: 16, 59: 17, 61: 18, 67: 19, 71: 20, 73: 21, 79: 22, 83: 23, 89: 24, 97: 25, 101: 26, 103: 27, 107: 28, 109: 29, 113: 30}
p = 109
print "%d ist die %d. Primzahl" % (p, primzahlen[p]) 
        
109 ist die 29. Primzahl
109 ist die 29. Primzahl

Mengen

s1 = set([1..10])
s2 = set([5..15])
s3 = set([1, 1, 1, 1])
s1; s2; s3 
        
set([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
set([5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15])
set([1])
set([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
set([5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15])
set([1])
s1.union(s2) 
        
set([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15])
set([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15])
s1.intersection(s2) 
        
set([5, 6, 7, 8, 9, 10])
set([5, 6, 7, 8, 9, 10])
s1.symmetric_difference(s2) 
        
set([1, 2, 3, 4, 11, 12, 13, 14, 15])
set([1, 2, 3, 4, 11, 12, 13, 14, 15])

Kontrollstrukturen

Python die Programmiersprache von Sage verwendet Einrückungen zur Definition von Blöcken.

If-Statement

For-Schleife

for i in [1,2,3,4]:
 j = i^2
 print j 
        
1
4
9
16
1
4
9
16

While-Schleife

i = 1
while i < 20:
 if i.is_prime():
   print "%2d ist eine Primzahl" % i
 i += 1 
        
2 ist eine Primzahl
 3 ist eine Primzahl
 5 ist eine Primzahl
 7 ist eine Primzahl
11 ist eine Primzahl
13 ist eine Primzahl
17 ist eine Primzahl
19 ist eine Primzahl
2 ist eine Primzahl
 3 ist eine Primzahl
 5 ist eine Primzahl
 7 ist eine Primzahl
11 ist eine Primzahl
13 ist eine Primzahl
17 ist eine Primzahl
19 ist eine Primzahl

Definieren von Funktionen

Selbstdefinierte Funktionen funktionieren automatisch für alle Typen, die alle in der Funktion verwendeten Methoden und Operationen unterstützen.
In unserem Beispiel:
  • Vergleichsoperator <
  • Negation -
R = RealField(prec = 200)
absolutbetrag(R.random_element(-10, -5)) 
        
6.3143950641973070900223374505923141912547366595474086604627
6.3143950641973070900223374505923141912547366595474086604627