Franz Lehner
List of Publications
- with Kamil Szpojankowski: Free Integral Calculus I, arXiv:2311.04039.
- with Octavio Arizmendi and Amnon Rosenmann: On matrices in finite free position, Lin Alg Appl 724 (2025) 137-170, arXiv:2309.14343.
- with Octavio Arizmendi and Takahiro Hasebe: Cyclic independence: Boolean and monotone, Alg Comb 6 (2023) 1697-1734, arXiv:2204.00072.
- with Jean-Christophe Novelli and Jean-Yves Thibon: Combinatorial Hopf algebras in noncommutative probability, arXiv:2006.02089, in progress.
- with Wiktor Ejsmont: The Free Tangent Law, Adv Appl Math 121 (2020) 102093, arXiv:2004.02679.
- with Wiktor Ejsmont: The Trace Method for Cotangent Sums, J Comb Th A 177 (2021) 105324, arXiv:2002.06052.
- with Wiktor Ejsmont: Sums of Commutators in Free Probability, J Funct Anal (2020) 108791, arXiv:2002.06051.
- with Kamil Szpojankowski: Boolean Cumulants and Subordination in Free Probability, Random Matrices: Theory and Applications (RMTA) 2021 , to appear, arXiv:1907.11442.
- with Amnon Rosenmann and Aljosa Peperko: Polynomial convolutions in max-plus algebra, Lin Alg Appl 578 (2019) 370-401, arXiv:1802.07373.
- with Takahiro Hasebe: Cumulants, Spreadability and the Campbell-Baker-Hausdorff Series, arXiv:1711.00219.
- with Wiktor Ejsmont: Sample Variance in Free Probability, J. Funct. An. 273 (2017) 2488-2520, arXiv:1607.06586.
- with Octavio Arizmendi, Takahiro Hasebe, and Carlos Vargas: Relations between cumulants in noncommutative probability, Adv.Math.282 (2015) 56-92, arXiv:1408.2977.
- Free Nested Cumulants and an Analogue of a Formula of Brillinger, Prob.Math.Stat. Vol. 33 (2013), Fasc. 2, 327-339, arXiv:1312.5671.
- with Stephan Wagner: Free Lamplighter Groups and a Question of Atiyah, Amer. J. Math. 135 (2013), no. 3, 835–849, arXiv:1005.2347,
- with Gennadii Chistyakov and Friedrich Goetze: Freeness of Linear and Quadratic Forms in von Neumann Algebras, J. Funct. An. 261 (2011), no. 10, 2829-2844, arXiv:1012.5586.
- Cumulants as iterated integrals, J. Stat. Plann. Inf. 141, Issue 4 (2011), 1448-1454, arXiv:0905.3375.
- A noncrossing basis for noncommutative invariants of SL(2,C), J. Comb. Th. A 118 (2011), no. 1, 257-269, arXiv:0905.1860.
- with Serban Belinschi, Marek Bozejko and Roland Speicher: The normal distribution is $\boxplus$-infinitely divisible, Adv. Math. 226, Issue 4 (2011), 3677-3698, arXiv:0910.4263.
- with Michael Anshelevich, Serban Belinschi and Marek Bozejko: Free Infinite Divisibility for Q-Gaussians, Math. Res. Lett. 17, no.05, (2010), 905-916, arXiv:1003.0935,
- On the eigenspaces of lamplighter random walks and percolation clusters on graphs, Proc. AMS 137 (2009), no. 8, 2631-2637, arXiv:0805.0867.
- with Wolfgang Woess and Markus Neuhauser: On the spectrum of lamplighter groups and percolation clusters, Math. Ann. 342 (2008), no. 1, 69-89, arXiv:0712.3135.
- with Marek Bożejko and Ken Dykema: Isomorphisms of Cayley graphs of surface groups., Algebra Discrete Math. 2006, no. 1, 18-37.
-
Cumulants in noncommutative probability theory I. Noncommutative Exchangeability Systems,
Math. Z. 248 (2004), no. 1, 67-100,
arXiv:math.CO/0110442.
Abstract: Cumulants linearize convolution of measures. We use a formula of Good to define noncommutative cumulants in a very general setting. It turns out that the essential property needed is exchangeability of random variables. Roughly speaking the formula says that cumulants are moments of a certain ``discrete Fourier transform'' of a random variable. This provides a simple unified method to understand the known examples of cumulants, like free cumulants and various q-cumulants.
-
Cumulants in noncommutative probability theory II. Generalized Gaussian random variables, Probab. Theory Related Fields 127 (2003), no. 3, 407-422,
arXiv:math.CO/0110443.
Abstract: We continue the investigation of noncommutative cumulants. In this paper various characterizations of noncommutative Gaussian random variables are proved.
-
Cumulants in noncommutative probability theory III. Creation- and annihilation operators on Fock spaces,
Infin. Dimens. Anal. Quantum Probab. Relat. Top. 8 (2005), no. 3, 407-437,
arXiv:math.CO/0110444.
Abstract: Fock space constructions give rise to natural exchangeable families and are thus well suited for cumulant calculations. In this paper we develop some general formulas and compute cumulants for generalized Toeplitz operators, notably for q-Fock spaces, previously considered by M. Anshelevich and A. Nica.
- Cumulants in noncommutative probability theory. IV. Noncrossing cumulants: De Finetti's theorem and Lp-inequalities., J. Funct. Anal. 239 (2006), no. 1, 214-246, arxiv:math/0409025.
-
Cumulants, lattice paths, and orthogonal polynomials.
Discrete Math. 270 (2003), no. 1-3, 177-191,
arXiv:math.CO/0110031
or see the slides from my talk at MSRI.
Abstract: A formula expressing free cumulants in terms of the Jacobi parameters of the corresponding orthogonal polynomials is derived. It combines Flajolet's theory of continued fractions and Lagrange inversion. For the converse we discuss Gessel-Viennot theory to express Hankel determinants in terms of various cumulants.
-
Free cumulants and enumeration of connected partitions.
Europ. J. Combinatorics 23 (2002), 1025-1031,
arXiv:math.CO/0110030.
Abstract: A combinatorial formula is derived which expresses free cumulants in terms of classical comulants. As a corollary, we give a combinatorial interpretation of free cumulants of classical distributions, notably Gaussian and Poisson distributions. The latter count connected pairings and connected set partitions respectively. The proof relies on Moebius inversion on the partition lattice.
-
On the computation of spectra in free probability,
Journal of Funct. An. 183 (2001) pp.451-471,
arXiv:math.OA/0008084
Abstract: We use free probability techniques to compute borders of spectra of non hermitian operators in finite von Neumann algebras which arise as "free sums" of "simple" operators. To this end, the resolvent is analyzed with the aid of the Haagerup inequalidty. Concrete examples coming from reduced C*-algebras of free product groups and leading to systems of polynomial equations illustrate the approach.
- with Philippe Biane: Computation of some Examples of Brown's Spectral Measure in Free Probability.
Coll. Math. 90 (2001) 181-211,
arXiv:math.OA/9912242,
ESI Preprint 823.
Abstract: We use free probability techniques for computing spectra and Brown measures of some non hermitian operators in finite von Neumann algebras. Examples include
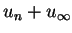 where
where 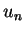 and
and
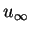 are the generators of Zn and Z respectively,
in the free product Zn*Z, or elliptic elements,
of the form
are the generators of Zn and Z respectively,
in the free product Zn*Z, or elliptic elements,
of the form
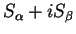 where
where
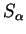 and
and 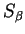 are free
semi-circular elements of variance
are free
semi-circular elements of variance 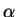 and
and 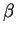 .
.
- Computing norms of free operators with matrix coefficients.
Amer. J. Math. 121 (1999) 453-486.
Abstract: Let
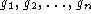 be the generators of the free group
be the generators of the free group
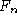 and
denote by
and
denote by 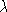 its left regular representation.
A formula for norms of operators of the form
its left regular representation.
A formula for norms of operators of the form
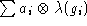 where
where
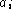 are complex matrices or operators
is derived similar to the formula of Akemann and Ostrand for the scalar case. This formula can
be used to compute norms of arbitrary finitely supported convolution operators on the free group.
Essentially the same technique yields a
formula for the norms of sums of matrix valued creation and annihilation operators on full Fock space. In a
final section, some results about numerical evaluation of the formula are proved.
are complex matrices or operators
is derived similar to the formula of Akemann and Ostrand for the scalar case. This formula can
be used to compute norms of arbitrary finitely supported convolution operators on the free group.
Essentially the same technique yields a
formula for the norms of sums of matrix valued creation and annihilation operators on full Fock space. In a
final section, some results about numerical evaluation of the formula are proved.
- dvi:(139 Kb)
- PostScript gzip file (164 Kb)
- A characterization of the Leinert property.
Proc. Amer. Math. Soc. 125 (1997), no.
11, 3423-3431.
Abstract: Let G be a discrete group and denote by
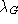 its left regular
representation on
its left regular
representation on 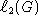 . Denote further by
. Denote further by 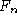 the free group
on n generators
the free group
on n generators 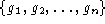 and
and 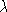 its left regular
representation.
In this paper we show that
a subset
its left regular
representation.
In this paper we show that
a subset 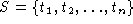 of G
has the Leinert property if and only if for some real positive coefficients
of G
has the Leinert property if and only if for some real positive coefficients
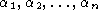 the identity
the identity
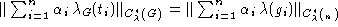 holds.
Using the same method we obtain some metric estimates about abstract
unitaries
holds.
Using the same method we obtain some metric estimates about abstract
unitaries 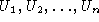 satisfying the similar identity
satisfying the similar identity
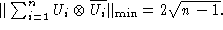
- Free operators with operator coefficients Colloquium Mathematicum, 74 (1997), 321-328.
Abstract: Let
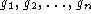 be the generators of the free group
be the generators of the free group 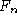 and
denote by
and
denote by 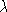 its left regular representation.
An inequality for norms of operators of the form
its left regular representation.
An inequality for norms of operators of the form
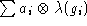 (for special
(for special 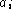 )
similar to the formula of Akemann and Ostrand for the scalar case is obtained,
however
an example shows that strict inequality can occur.
As a corollary we get the optimal constant in an inequality of
Haagerup and Pisier.
)
similar to the formula of Akemann and Ostrand for the scalar case is obtained,
however
an example shows that strict inequality can occur.
As a corollary we get the optimal constant in an inequality of
Haagerup and Pisier.
-
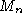 -
espaces, sommes d'unitaires et analyse harmonique sur le groupe libre [
-
espaces, sommes d'unitaires et analyse harmonique sur le groupe libre [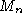 -spaces, sums of unitaries and harmonic analysis on the free group]. Ph.D. thesis, defended in Paris on september 22, 1997.
-spaces, sums of unitaries and harmonic analysis on the free group]. Ph.D. thesis, defended in Paris on september 22, 1997.
dvi:(142 Kb), PDF:
PostScript:
Preface (102 Kb)
Chapter 1: M_n spaces (197 Kb)
Chapter 2: sums of unitaries and harmonic analysis on the free group (175 Kb)
Bibliography(30 Kb)Abstract The first part of the thesis investigates
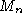 -spaces and their connections
with operator spaces and Banach spaces. An
-spaces and their connections
with operator spaces and Banach spaces. An 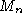 -space is defined as a Banach
space X together with a norm on the space of n times n matrices with entries
in X satisfying some Ruan-type conditions.
We develop a theory inspired by Blecher's and Paulsen's results on operator
spaces
including dual spaces and maximal and minimal operator space structures
associated to an
-space is defined as a Banach
space X together with a norm on the space of n times n matrices with entries
in X satisfying some Ruan-type conditions.
We develop a theory inspired by Blecher's and Paulsen's results on operator
spaces
including dual spaces and maximal and minimal operator space structures
associated to an 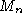 -space.
Another section is dedicated to certain norms on tensor products of
-space.
Another section is dedicated to certain norms on tensor products of 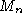 -spaces,
which we call reasonable, where analogues of the Haagerup tensor product
generalize the injective and projective tensor products of Banach spaces.
-spaces,
which we call reasonable, where analogues of the Haagerup tensor product
generalize the injective and projective tensor products of Banach spaces.
In the second part of the thesis we investigate a recent inequality for the norms of sums of certain unitaries. The combinatorial principle behind this inequality turns out to be the concept of nonnegative alternating mixed moments, which is studied in the first section. We then show that in the case of convolution operators on discrete groups equality takes place in this inequality if and only if the support of the operator in consideration satisfies the Leinert property, generalizing a result of Kesten. We give a counterexample to a conjectured generalization of this result about the structure of unitaries for which the above inequality turns into an equality, involving the representations of the free group constructed by Pytlik and Szwarc. However, we show some inequalities for subfamilies of families of unitaries whose sum attains minimal norm. Finally, an inequality for the norms of matrix-valued free operators is derived, which yields the optimal constant in an inequality by Haagerup and Pisier.